谷山公規（たにやま こうき） 教育・総合科学学術院教授

（１）はじめに

一見すると何でもない簡単な体の動きの中に幾何学の原理が秘められていることを解説します。

（２）体操実演

まず（片手でもいいのですが）両手を体の前に伸ばします。このとき指先は揃えて真直ぐ前方に伸ばし、手のひらは下を向くようにします（写真１）。次に両手を伸ばしたまま真上まで持ち上げます。その際腕はねじらずにそのまま持ち上げます。このとき指先は天を指し、手のひらは正面を向いています（写真２）。次に両手を伸ばしたまま左右に降ろして体の真横に来るまで持って来ます。その際にも腕はねじりません。すると依然として手のひらは正面を向いています（写真３）。最後に両手を伸ばしたまま水平に動かして体の前まで持って来ます。この際にも腕はねじりません。これで両手は最初の位置に戻ってきました。ところが両手のひらは最初は下を向いていたのに今度は向かい合っています。つまりそれぞれ９０°ねじれた訳です（写真４）。ここまでの動きを「体操その１」と呼ぶことにします。

手のひらの向きはそのままで、もう一度同じことを繰り返します。すると今度は手のひらは上を向きます（写真４～７）。また９０°ねじれた訳です。さらにもう一度同じことを繰り返すには関節が相当柔らかくないと出来ません。

途中ではねじっていないのに、腕が元の位置に戻ったときに９０°ねじれてくるのは不思議ですね。どうしてでしょうか。

今度は違う動きで試してみましょう。立った姿勢で両手は下に降ろします。手のひらは後を向くようにしておきます。それから両手を伸ばしたまま前方に持ち上げていき、途中で止めずにそのまま真上まで持ち上げます。このとき手のひらは正面を向いています。次に両手を左右に開いて下に降ろします。すると手のひらは正面を向いています。つまり今回は一度に１８０°ねじれたことになります。これを「体操その２」と呼ぶことにします。

もう一つ違う動きを実験してみましょう。「体操その１」のように両手を前方に伸ばし、手のひらは下に向けておきます。ここから両手を上に持ち上げますが、今度は真上まで行かずに斜め４５°で止めます。次にその位置から両手を左右に切り降ろして体の真横に持って来ます。このとき手のひらは斜め４５°下を向いています。次に両手を水平に動かして体の前に持って来ると、今度は手のひらは斜め４５°になっています。つまり最初の状態から比べてねじれた角度は４５°です。これを「体操その３」と呼ぶことにします。

（３）体操の幾何学的説明

　実はこれらの現象は幾何学で説明出来るのです。これらの体操では指先は、肩を中心として腕の長さを半径とする球面上を動いていることに注目します。

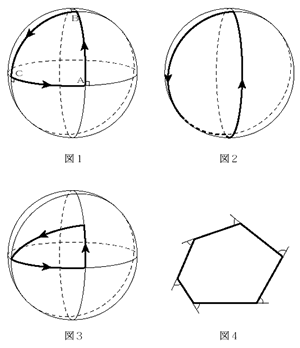
球面上で２点を結ぶ最短距離の曲線を測地線といいます。測地線は、球面を球面の中心を通る平面で切ったときの切り口として現れる円（これを大円と呼びます）の一部分となります。球面上で、何本かの測地線で囲まれた図形を球面多角形と呼びます。「体操その１」（の右手の動きだけを考えたもの）は、肩を中心として腕の長さを半径とする球面を８等分して得られる球面三角形（図１）に沿って手を動かしたものになっています。「体操その２」は球面を４等分して得られる球面二角形（図２）に、「体操その３」は図１の球面三角形をさらに２等分して得られる球面三角形（図３）に対応しています。腕のねじれる角度と球面多角形の面積が比例していますね。

平面上に多角形があったときに、その外角和（図４）が３６０°になることは中学の数学で習われた方も多いと思います。ところが球面多角形の外角和は３６０°より小さくなります。どのくらい小さくなるかはその球面多角形の面積に比例します（このことは、球面三角形の面積と内角和に関する有名な公式を使えばすぐに証明出来ます）。実はその３６０°から外角和を引いた角度が腕のねじれの角度と一致するのです。このことを「体操その１」を例にとって説明してみましょう。図１で頂点Ａから出発したとき、手の進む向きと手の甲の向きは一致しています。頂点Ｂで曲がる際に手の進む向きと手の甲の向きにずれが生じます。その角度が頂点Ｂにおける外角、すなわち９０°です。さらに頂点Ｃで曲がる際には、手の進む向きと手の甲の向きのずれに頂点Ｃにおける外角９０°が加算され、手の進む向きと手の甲の向きは正反対すなわち１８０°となります。最後に手が頂点Ａに戻ってきたときに頂点Ａにおける外角９０°が加算され、ふたたび頂点Ｂへ向かって手の進む向きと手の甲の向きのずれは２７０°となります。この２７０°が図１の球面三角形の外角和です。もしもこの外角和が３６０°であれば手の進む向きと手の甲の向きはふたたび一致しているはずですが、足りない９０°分だけ手の進む向きと手の甲の向きがずれてしまっています。すなわち９０°だけ手がねじれた訳です。

一般に「曲面上の測地多角形の外角和を３６０°から引いた値は、その多角形上の各点でのガウス曲率を面積分した値に等しい」 ということがガウス－ボンネの定理という微分幾何学の美しい定理として知られています。ですから腕がねじれてくる原因を微分幾何学的に述べれば「球面上の各点のガウス曲率が正であるから」ということになります。小さく「球面幾何体操」と命名してもよかったのですが、せっかくなので、曲面の曲率を体感するという意味まで込めて、大きく「微分幾何体操」と命名しました。実際私自身この微分幾何体操を思いついたことによって曲面のガウス曲率についての理解を深めることが出来ました。

（４）終わりに

以上の説明でお分かりいただけたでしょうか。理論はともかく、実際に体を動かしてみて「不思議だな」と思っていただければ、そして少しでも幾何学や数学に興味を持っていただけたらと思います。

余談ですが、肩の代わりに肘を中心として動かす「微分幾何体操第２」もあります。この第２を片手だけで繰り返し行なうと「一人合気道」になります。試してみてください（笑）。また、「体操その１」やその逆の動きを、適当な重さのダンベルを持って行なうと、腕のいろいろな筋肉を順番に鍛えることが出来て便利です。ときどき私は実行しています。関節をねじることは身体に間接的な刺激を与えて健康にも良いです。

以上が微分幾何体操の説明でした。まあ、そんなたいそうなものではありませんけれど。

略歴

早稲田大学教育・総合科学学術院教授。
早稲田大学教育学部理学科数学専修卒業。
早稲田大学大学院理工学研究科博士課程数学専攻修了。
博士（理学）。
東京女子大学文理学部専任講師、同助教授、 早稲田大学教育学部助教授を経て現職。
専門：位相幾何学－結び目理論－空間グラフ理論。
１９９７年度日本数学会賞建部賢弘賞受賞。

著作

A partial order of knots, Tokyo Journal of Mathematics, 12, (1989), 205-229. Cobordism, homotopy and homology of graphs in $R^3$, Topology, 33, (1994), 509-523. など。

（2006年9月4日更新）
※この特集はasahi.comに2002年10月～2008年3月まで掲載されたものです。
※掲載内容を早稲田大学と朝日新聞社に無断で転載することを禁じます。