2値分類器の結合による多値分類法の理論的解析に成功

深層学習モデルにおける性能向上に期待

発表のポイント

機械学習分野において、2値分類器を組み合わせて多値分類器を構築するError-correcting output coding (ECOC)は実験的に良い性能を示すことが知られていましたが、その理由は理論的に明らかになっていませんでした。

本研究では２値分類器の推定性能に着目し、その推定誤差に対して頑健なECOCの枠組みを数理的にモデル化することで、分類誤り率を最小とする最大事後確率分類に限りなく近づける方法を理論的に明らかにしました。

近年脚光を浴びている深層学習モデルに本研究成果を適用することにより、その性能向上に大きく寄与することが期待されています。

早稲田大学データ科学センター講師 雲居 玄道（くもい げんどう）、電気通信大学大学院情報理工学研究科准教授 八木 秀樹（やぎ ひでき）、および早稲田大学データ科学センター教授 小林 学（こばやしまなぶ）、早稲田大学理工学術院創造理工学部教授 後藤 正幸（ごとう まさゆき）、早稲田大学名誉教授 平澤 茂一（ひらさわ しげいち）による共同研究グループは、2値分類器を組み合わせて多値分類器を構築するError-correcting output coding (以下、「ECOC」)の枠組みを数理的にモデル化し、ECOCが良い分類性能を示すための、2値分類器の組み合わせの条件を理論的に明らかにしました。

本研究成果は、シンガポール・World Scientific社発行の『International Journal of Neural Systems, Vol. 33, No. 2 (2023) 』に、論文名 “Performance Evaluation of Error-Correcting Output Coding Based on Noisy and Noiseless Binary Classifiers” として掲載されました。

（１） これまでの研究で分かっていたこと（科学史的・歴史的な背景など）

機械学習分野において、データに紐づけられた内容を表すカテゴリを学習し、新しい入力データのカテゴリを推定する分類問題は大きなテーマの１つです。対象とするカテゴリ数が２つのものを2値分類問題、3つ以上のものを多値分類問題と呼びます。このカテゴリ数が多くなるほど問題が複雑になるため、分類問題を解決するには多くの困難があります。

この多値分類問題を解決する方法の１つに、2値分類問題の組み合わせと捉えるECOCが1994年にT. G. Dietterichらによって示されました（図１）。ECOCは符号理論における誤り訂正の考え方を援用した方法で、複数の2値分類器を用いることで、いくつかの2値分類器の出力が間違っていても正しいカテゴリを推定することができるという仕組みです。

そのため、多値分類を2値分類として様々なパターンに2値変換して2値分類器を構築します。例えば、カテゴリ数が４の場合、最も単純な方法は、2値変換に4つのカテゴリを１対3に分割する４種類の2値分類器を用いる方法でOne-vs-Restと呼ばれます。これ以外に、2対2に分ける2-vs-Restが考えられ、最大で7種類の2値分類器を用いることが可能です（図2）。この最大の2値分類器数をもつExhaustive Codeから良い性能を示す2値分類器の組み合わせを選択することがECOCの大きな課題です。そのため、多くの研究が成され、様々なデータに対してECOCが良い性能を示すことは実験的に知られています。しかし、実験条件を変えれば良い性能を示す2値分類器の組み合わせが変わることから、2値分類器の組み合わせ方法の明確な答えは示されていませんでした。

（２） 今回の研究で新たに実現しようとしたこと、明らかになったこと

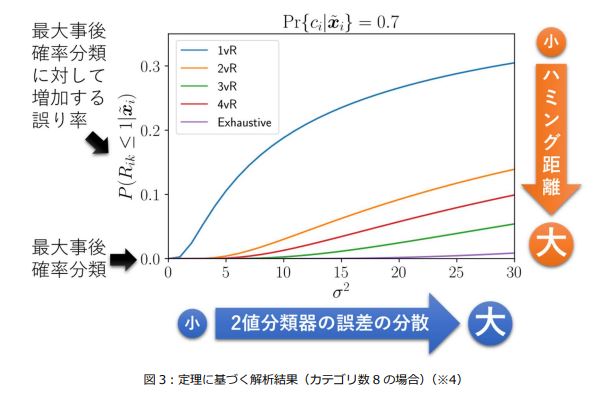
本研究では、よい性能を示す2値分類器の組み合わせを明らかにするべく、2値分類器の推定性能に着目しました。一般的にデータから分類規則を学習した2値分類器は、データの不足などから推定誤差が生じると考えられます。この推定誤差に対して頑健な2値分類器を組み合わせるための条件を明らかにしました。この結果、2値分類器の構成を示す符号語表（※1）に対し、符号語間のハミング距離（※2）を大きくすれば、2値分類器の誤差の分散が大きくなったとしても分類誤り率を最小とする最大事後確率分類（※３）に限りなく近づくことを明らかにしました（図3）。

（３） そのために新しく開発した手法

従来、ECOCの理論的解析が困難であった理由は、分類問題がもつ複雑性が要因であると考えられます。この原因は、データに含まれるノイズと2値分類器の推定誤差であるノイズが混在しているため、実験では実験条件に依存した結果しか得られていなかったことと考え、この2種のノイズを仮定した数理モデルを新たに考案しました（図4）。

この数理モデルに基づき、本研究では2値分類器のノイズに統計的な性質を仮定し、符号語間のハミング距離を用いてカテゴリ間の分類誤り率を解析する手法を開発しました。

（４） 研究の波及効果や社会的影響

本研究は、実データに対する実験結果から性能が良いとされてきたECOCに対し、理論的な保証を与えるものです。そのため、ECOCを実応用に適用する際に、想定される2値分類器の誤差や計算機環境に応じて、本研究の成果を用いて組み合わせる2値分類器を決定することが可能になります。

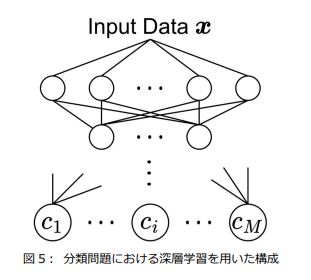
さらに、近年脚光を浴びている深層学習モデルも分類問題に適用する場合、多くの場合で出力層は図2に示したOne-vs-Restの形をとります（図5）。そのため、深層学習モデルもECOCの枠組みで捉えることが可能になることから、数多の深層学習モデルに対して、本研究の知見を適用することで性能向上をはかれる可能性があります。

（５） 今後の課題

本研究で示した理論的解析には、さまざま仮定を設定しています。そのため、ECOCにおける全てが明らかになったわけではありません。今後は、設定した仮定による制約を緩めるなど、より広い範囲で性能解析が可能な数理モデルを構築していきたいと考えております。

（６） 研究者のコメント

複雑な分類問題の研究に新たな解析手法を提案しました。この研究は、理論的解析が困難であったこの分野に一石を投じるものです。この研究成果は、石の上にも三年といった状況でようやく達成されました。この経験から、何事も軽々しく判断せず、物事の本質をしっかりと見極めることが大切であることを学びました。

 （７） 用語解説

※1　符号語表

ECOCにおいて2値分類器の構成を示す表のことです。例えば、図1に示す表のことであり列が2値分類器を意味します。行は各カテゴリに対応付けられており、各行が符号語と呼ばれます。

※2　ハミング距離

符号語間の0,1の異なっている数のこと。例えば、図1の符号語表のハミング距離は、すべての符号語間で4となります。

 ※3　最大事後確率分類

入力データ に対して，各カテゴリの真の事後確率 の最大値をとるカテゴリに分類することです。

※4 Exhaustive

Exhaustive Codeとは、構成可能な全ての2値分類器を用いたものです。図3に示したカテゴリ数8の場合は、1vR，2vR，3vR，4vRに含まれる2値分類器を全て用いたものです。

 （８） 論文情報

雑誌名：International Journal of Neural Systems
論文名：Performance Evaluation of Error-Correcting Output Coding Based on Noisy and Noiseless Binary Classifiers
著者名：雲居玄道（早稲田大学データ科学センター講師（任期付））、八木秀樹（電気通信大学大学院情報理工学研究科准教授）、小林学（早稲田大学データ科学センター教授）、後藤正幸（早稲田大学理工学術院創造理工学部教授）、平澤茂一（早稲田大学名誉教授）
掲載日時（現地時間）：2023年1月9日（月）※オンライン
掲載URL：https://www.worldscientific.com/doi/10.1142/S0129065723500041
DOI：10.1142/S0129065723500041

（９） 研究助成

研究費名：日本学術振興会（JSPS）科学研究費 (基盤研究C)
研究課題名：ビジネス価値創造のためのデータ解析プラットフォームと時変協調フィルタリングの研究
研究代表者名（所属機関名）：小林学（早稲田大学）

研究費名：日本学術振興会（JSPS）科学研究費 (基盤研究C)
研究課題名：高信頼・高安全な符号化システムの実現に向けた理論展開
研究代表者名（所属機関名）：八木秀樹（電気通信大学）