イジング計算機で組合せ最適化問題の「真の最適解」を高精度に探索

局所最適解から効率よく脱出する技術を開発

発表のポイント

現状のイジング計算機は、真の最適解を探索する途中に局所最適解から抜け出せないという問題があった。

本研究では、二つあるいはそれ以上のスピンを結合して一つのスピンとして扱う手法を開発することで、局所最適解から脱出し真の最適解を得やすくする仕組みを構築し、この仕組みをイジング計算機に組み込むためのアルゴリズムを開発した。

本技術をさまざまなイジング計算機に適用することで、高精度に現実世界の組合せ最適化問題を解くことができ、同時に将来のイジング計算機アーキテクチャの発展にも大きく寄与する。

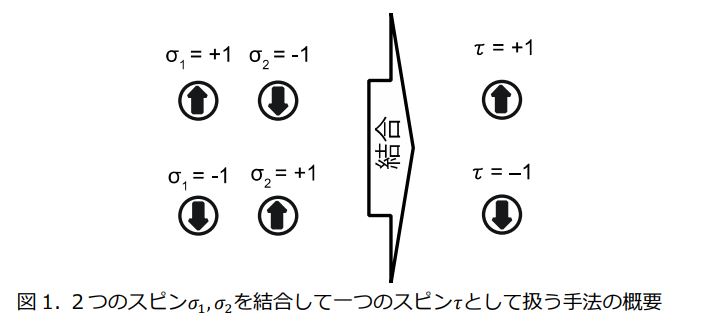
イジング計算機^※1は、真の最適解を探索する途中に局所最適解^※2から抜け出せないという問題がありました。これを解消するため、早稲田大学理工学術院講師の白井達彦（しらい たつひこ）氏，同大学理工学術院教授の戸川望（とがわ のぞむ）氏らの研究グループは、二つあるいはそれ以上のスピン（イジング計算機の計算の単位、各スピンは＋１あるいは−１の値をもつ）を結合して一つのスピンとして扱うこと（図１）で、局所最適解から抜け出し真の最適解を得やすくする仕組みを開発しました。さらに、本研究グループは、この仕組みをイジング計算機に適用するためのアルゴリズムを開発し、計算機シミュレータおよび既存イジング計算機でその有効性を確認しました。

本研究成果は、米国のIEEE Computer Societyが発行する『IEEE Transactions on Computers』online版（Early Access）に2022年5月27日（金）付（現地時間）で掲載されました。

論文名：Multi-spin-flip engineering in an Ising machine

（１）　これまでの研究で分かっていたこと（科学史的・歴史的な背景など）

現実世界のあらゆるところに存在する組合せ最適化問題^※3は大規模になるほど、従来型のコンピュータで最適解を得ることが困難になるため、さまざまな解法が研究されています。中でも近年、量子アニーリングマシン^※4をはじめとしたイジング計算機と呼ばれる新しいタイプの計算機が注目されています。イジング計算機は組合せ最適化問題の答えを得るのに特化した計算機です。イジング計算機は国内外で研究開発され、一般のユーザーもクラウド上で使用できる段階になっています。

しかし、イジング計算機を活用するにはまだ課題が多くあります。特に、多くのイジング計算機は、スピンの値を一つずつ反転して（+1を-1にする、あるいは-1を+1にすること）解の探索が行われていますが、一つのスピンを反転させるだけでは局所最適解から抜け出せないという問題がありました。既存研究では、複数のスピンを同時に反転させることによって局所最適解から抜け出す方法が提案されていましたが、その手法を既存のイジング計算機へ実装することはハードウェアコストが高く非常に困難でした。

（２）　今回の研究で新たに実現しようとしたこと、明らかになったこと

今回の研究では、スピンを一つずつ反転することで解を探索するイジング計算機において、複数のスピンを同時に反転させるのと同等の効果を得るための仕組みを実現しようと試みました。そのために、二つあるいはそれ以上のスピンを結合して一つのスピンとして扱う手法を開発しました。これにより、一つのスピンを反転させることによって複数のスピンを同時に反転させるのと同等の効果を得ることができます。たとえば、図１でスピン を から に反転することは、スピン を から に、そしてスピン を から に同時に反転することに対応します。

さらに、今回の研究では、この仕組みをイジング計算機に組み込むためのアルゴリズムも提案しました。スピンの結合はイジング計算機の外部で実行できるため、既存のさまざまなイジング計算機ハードウェアを作り替えることなく、本研究の仕組みを導入することができます。また、提案したアルゴリズムは局所最適解から効率よく抜け出すことができます。仕組みを組み込まない場合と比較して、残留エネルギー^※5を平均して86%削減することが明らかになりました。

 （３）　そのために新しく開発した手法

複数のスピンを一つのスピンに結合する手法を用いて組合せ最適化問題をイジング計算機で解くことを考えます。この際、どのスピンとどのスピンとを結合するかがポイントとなります。このとき、イジング計算機の性能を上げるためには、局所最適解から抜け出すようにスピンの集まりを結合する必要があります。

そこで、組合せ最適化問題に現れる制約に着目します。このとき解は制約を満たす解と制約を満たさない解の二つに分けることができます。多くの場合、制約を満たす解は局所最適解となります。いま、解が制約を満たす解であると仮定します。イジング計算機から出力される解の多くはこの仮定を満たします。そこで、別の制約を満たす解を考え、その解に移るために反転させる必要のあるスピンの集まりを探します。そのスピン同士を結合させることによって、局所最適解を脱出して制約を満たす解の間を探索することが可能となります。このように、イジング計算機から出力される局所最適解と制約を満たす解空間の構造とを考慮することで、結合するスピンの集まりを決定することが可能となります。

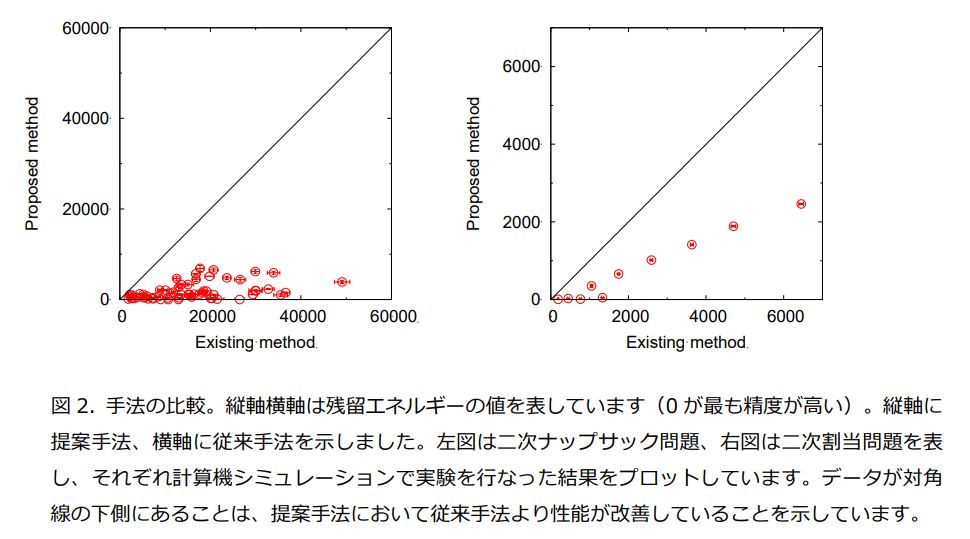
実際に、イジング計算機で解法することが困難とされる異なる二つのタイプの組合せ最適化問題に対して、本手法を組み込んだ場合（提案手法）と組み込まなかった場合（従来手法）とを残留エネルギーで比較しました。その結果、二次ナップサック問題^※6で平均して残留エネルギーを89%削減し、二次割当問題^※7で平均して残留エネルギーを67%削減し、提案アルゴリズムの有効性が確認できました（図2）。

（４）　研究の波及効果や社会的影響

本手法を使うことによって、スピンの値を一つずつ反転して解を探索するイジング計算機を用いて、複数のスピンを同時に反転して解を探索するのと同等の探索方法を実現することができます。スピンを結合する今回の新しい手法は、拡張性が高く既存のイジング計算機に簡単に導入することができることから、近いうちにイジング計算機の発展に大きく寄与することが期待できます。あるいは、今後、新規にイジング計算機が開発される際に、本手法を取り込んだイジング計算機が開発される可能性があります。例えば、今回の手法により配送計画の最適化が実現すると、二酸化炭素排出量の削減など社会的問題へ大きく貢献する可能性があります。

（５）　今後の課題

本手法は、スピンの結合をCPUで、解の探索をイジング計算機で行なうため、CPUとイジング計算機の間の通信時間が増えるという問題があります。今後の研究では、両者をシームレスに繋ぐハードウェアアーキテクチャを設計する必要があります。また、実世界に見られるさまざまな問題に対し、本手法の有効性を検証していく必要があります。

 （６）　研究者のコメント

本研究ではイジング計算機の性能を改善するための手法を開発しました。本研究で開発した手法を使うことで、今後イジング計算機の性能がさらに改善し、新たにイジング計算機を活用できる事例が増えることを期待します。

 （７）　用語解説

※1　イジング計算機

組合せ最適化問題を「イジングモデル」で表現し、組合せ最適化問題を解決する計算機の総称。イジングモデルはもともと磁性を説明するモデルとして統計力学の分野で導入された。

※2　局所最適解

イジング計算機が探索可能である解のうち、その周囲の解と比較して、局所的に目的関数の値が小さい（または大きい）解。局所最適解は解空間の中にいくつも存在し、その中で目的関数の値を最小（または最大）とする解が真の最適解となる。

※3　組合せ最適化問題

膨大な選択肢の中から､与えられた制約を満たしつつ、関数の最小値（または最大値）をとる選択肢を求める問題の総称。

※4　量子アニーリングマシン

イジング計算機の一種。量子効果により量子重ね合わせ状態を実現させ、それを初期状態として用意し、徐々に量子効果を弱める。同時に組合せ最適化問題を表現するイジングモデルの効果を強めることにより、イジングモデルの安定状態を実現させるという機構で動作する。

※5　残留エネルギー

イジング計算機で組合せ最適化問題を解いた際に得られた解の精度を評価する指標の一つ。得られた解の目的関数の値と真の最適解の目的関数の値の差で与えられ、値が小さいほど解の精度が良いことを表す。

※6　二次ナップサック問題

ナップサックの中に入れた品物の重量の合計がナップサックの容量を超えてはいけないという制約のもとで、ナップサック内の品物の価値の合計を最大化する組合せ最適化問題。

※7　二次割当問題

工場と地点が同じ個数与えられたとき、各工場を各地点に割り当てたときの地点間の輸送コストの合計を最小化する組合せ最適化問題。

 （８）　論文情報

雑誌名：IEEE Transactions on Computers
論文名：Multi-spin-flip engineering in an Ising machine
執筆者名（所属機関名）：Tatsuhiko Shirai（早稲田大学）, Nozomu Togawa（早稲田大学）
※　所属は論文投稿時
掲載日（現地時間）：2022年5月27日（金）
掲載URL：https://ieeexplore.ieee.org/document/9783142
DOI：10.1109/TC.2022.3178325

（９）　研究助成（外部資金による助成を受けた研究実施の場合）

研究費名・研究課題名：科学技術振興機構（ＪＳＴ） 戦略的創造研究推進事業 ＣＲＥＳＴ「地理空間情報を自在に操るイジング計算機の新展開」（JPMJCR19K4）
研究代表者名：戸川望（早稲田大学・教授）

研究費名・研究課題名：基盤研究(C)「量子古典ハイブリッド計算技術による物質シミュレーション高速化手法の研究」
研究代表者名：田中宗（慶應義塾大学・准教授）
早稲田大学における研究代表者名：白井達彦（早稲田大学・講師）