アト秒レーザーで位相を分けた電子波動関数の直接イメージングに成功
新規なアト電子テクノロジーの開発に期待
 早稲田大学理工学術院の新倉弘倫(にいくらひろみち)教授は、カナダ国立研究機構 (National Research Council of Canada)、独マックス・ボルン研究所(Max Born Institute)と共同で、アト秒レーザー(高次高調波)によるネオン原子の光イオン化過程で生成した、ほぼ純粋なf-軌道電子(電子波動関数)の密度分布と、その位相を分けた波動関数に相当するイメージの直接測定に成功しました。またさらに、イオン化した電子波束がどのような位相と振幅を持つ波動関数から成っているかを同定する方法を開発しました。
早稲田大学理工学術院の新倉弘倫(にいくらひろみち)教授は、カナダ国立研究機構 (National Research Council of Canada)、独マックス・ボルン研究所(Max Born Institute)と共同で、アト秒レーザー(高次高調波)によるネオン原子の光イオン化過程で生成した、ほぼ純粋なf-軌道電子(電子波動関数)の密度分布と、その位相を分けた波動関数に相当するイメージの直接測定に成功しました。またさらに、イオン化した電子波束がどのような位相と振幅を持つ波動関数から成っているかを同定する方法を開発しました。
20世紀初頭に発達した量子力学によれば、原子・分子や電子などの極微の物質は波としての性質を持ち、波動関数(Ψ)で表されます。Max Bornの解釈では、電子波動関数の自乗(|Ψ|2)はその領域に電子が存在している確率を表しますが、波動関数そのものは複素数で記述され、振幅と位相によって特徴付けられています。例えば、波動関数の位相は、化学反応の選択性などを理解するのに重要ですが、直接の測定は困難でした(注1)。
今回の研究により、電子波動関数とその変化のイメージングを元にした新たなアト秒テクノロジーの発展が期待されます。
本研究成果は、2017年6月16日(現地時間)発行の米国科学誌『Science』に掲載されました。
背景
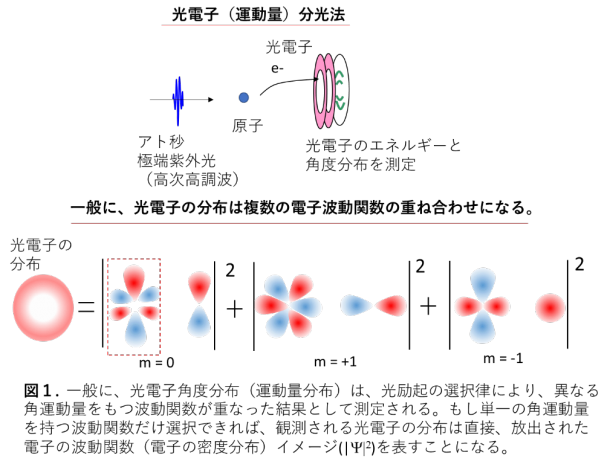
21世紀に入り、アト秒の科学が進展しています(注2)。アト秒の時間領域では、物質の構造変化よりも速い時間スケールで、原子や分子内の電子(波束)の動きを測定することが可能になります。アト秒のパルス幅を持つレーザーパルス(高次高調波と呼ばれます)は極端紫外領域の波長を持つため、物質に照射すると、光電子が放出されます(光イオン化過程)。放出された光電子のエネルギーや角度分布を測定(光電子分光法/光電子運動量分光法)することで、アト秒時間スケールでの物質の電子状態の変化を測定することが可能になっています。
一方、放出された光電子の角度分布(運動量分布)は、イオン化(励起)の選択律から、一般に複数の異なる角運動量を持つ量子状態(連続状態の電子波動関数)の重ね合わせになり、ブロードな分布を持ちます(図1)。したがって、個々の角運動量量子数(ℓ, m)を持つ波動関数を分けて測定することは困難でした。しかし、もし量子状態を選択して測定することが可能になれば、放出される光電子の運動量分布が直接、電子波動関数の分布を表すことになります。本研究では、アト秒高次高調波を用いた新たな概念に基づく測定方法を開発し、ネオン原子から放出されたほぼ純粋なf-軌道(ℓ=3, m=0)電子の確率分布(|Ψ|2)をイメージング測定しました。さらにアト秒パルスを追加することで、f-軌道の位相を分けた区別した波動関数(Ψ)に相当するイメージを得ることにも成功しました。
新規アト秒光学系の開発
高強度の赤外フェムト秒レーザー(基本波)を原子や分子に集光すると、高次高調波と呼ばれる、アト秒のパルス幅を持つ極端紫外領域のレーザーパルスが生じます(注3)。高次高調波をアト秒の時間分解測定に使うためには、一般に(1)基本波を二つに分ける、(2)片方の基本波で高次高調波を発生、(3)高次高調波を基本波から分離、(4)分けた基本波と高次高調波をアト秒精度で重ね合わせて測定試料に集光するという複雑な過程が必要になります。そのため、高精度で光学パスの安定性を保つためのフィードバック機構や、真空ポンプからの振動の分離などが必要であり、再現性のある長時間の安定した測定は困難でした。
本研究では、これらの複雑な過程を大幅に簡略化し、かつ高精度で原理的に時間差が変化しない、新たなアト秒光学系を開発しました。この装置系では、アト秒高次高調波と赤外光の時間差を50アト秒以下の精度で簡単に安定・制御できます。
本実験では、発生したアト秒高次高調波(パルス列)と赤外光(基本波)とを組み合わせて試料をイオン化し、放出された光電子の運動量分布を Velocity Map Imaging と呼ばれる光電子運動量測定装置で測定しました。なお本研究の実験はすべて、当研究室(新倉研究室、早稲田大学・西早稲田キャンパス51号館B19室)で開発した装置系を用いて行われたものです(図2)。

実験結果
(1)f-軌道(m=0)電子波動関数のイメージング
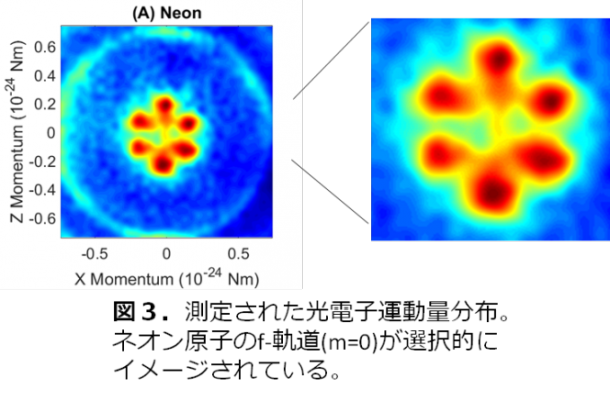 基本波(赤外パルス)の奇数次のみを含む高次高調波(アト秒パルス列)を発生し、基本波と組み合わせてネオンガスに照射したところ、図3に示すような光電子運動量分布を得ました(奇数次の高調波については注3参照)。6つの節がはっきりと観測されていますが、これはf-軌道(軌道角運動量量子数ℓ=3, 磁気量子数m=0)の特徴を示しています。
基本波(赤外パルス)の奇数次のみを含む高次高調波(アト秒パルス列)を発生し、基本波と組み合わせてネオンガスに照射したところ、図3に示すような光電子運動量分布を得ました(奇数次の高調波については注3参照)。6つの節がはっきりと観測されていますが、これはf-軌道(軌道角運動量量子数ℓ=3, 磁気量子数m=0)の特徴を示しています。
一般に、ネオン原子のように電子基底状態のp軌道からイオン化(励起)が行われると、異なる磁気量子数(m=1, m=0, m=-1)を持つd-軌道が同時に生成します。それらの寄与が重なるために、さらに1光子を吸収して放出される光電子の運動量分布はブロードになり、図3で測定されたようにm=0の分布だけを得ることはできません。本研究では、赤外光の強度と高次高調波の波長を変えて測定し、ある特定の範囲の強度と高次高調波の波長のときに、上記のようなf-軌道(m=0)が観測されることを発見しました。これは、図4に示すような機構によるものであると考えられます。すなわち(A)適切な強度の赤外パルスによるシュタルクシフトにより、異なる磁気量子数を持つエネルギー準位が分離される。(B)13次高調波(約20.5 eV)を用いて、ネオン原子の基底状態(1s)2(2s)2(2p)6から、シュタルクシフトによって分離した3d準位(m=0)に選択的に励起する。3d(m=0)準位から、赤外パルスによるイオン化によって、p-対称性とf-対称性を持つ電子波動関数が放出される。解析により、p-軌道の寄与は少なく、ほぼf-軌道のみが生成していることがわかりました。

(2) 位相を区別した波動関数イメージング
 図3で測定されたイメージは、波動関数の自乗(確率分布)に相当します。f-軌道は6つの節を持ちますが、節の両隣はそれぞれ異なる位相成分になっています。そこで次に、位相を分けた波動関数イメージの測定を行う方法を開発しました。
図3で測定されたイメージは、波動関数の自乗(確率分布)に相当します。f-軌道は6つの節を持ちますが、節の両隣はそれぞれ異なる位相成分になっています。そこで次に、位相を分けた波動関数イメージの測定を行う方法を開発しました。
アト秒高次高調波として、基本波の奇数次だけではなく、偶数次を同時に発生させ、赤外パルスと重ね合わせて試料に照射します(注3)。このとき、放出される光電子は、複数の量子パスによって生成した光電子の重ね合わせになります(図5)。すなわち(1)13次高調波と基本波(赤外光)の2光子イオン化過程により、f-軌道とp-軌道が生成する。(2)14次高調波により1光子イオン化過程により、p-軌道からはs-軌道とd-軌道が生成ししうる(詳細は後述:図5にはそれぞれf-軌道とs-軌道のみ記載)。イオン化により発生する電子波束は、これらの異なる角運動量を持つ電子波動関数(軌道)のコヒーレントな重ね合わせになります。
図5の右側に、s-軌道がf-軌道と重なった場合の模式図を示します。s-軌道は全対称であるため、波動関数の位相は一様に分布しています。したがって、f-軌道と足しあわされると同じ位相のみが強調され(図では赤の部分)、異なる位相成分はキャンセルしますので、f-軌道の位相を分けることが可能になります。ここで、赤外パルスと高次高調波の時間差をアト秒精度で制御することで、生成するf-軌道の位相を制御することが出来ます。ちょうどf-軌道の位相が反転したときにs-軌道を重ねると、異なる位相成分の組を抜き出すことが可能になります。
図6に、測定された光電子運動量分布を示します。ある特定の高次高調波と赤外光との時間差の時に、f-軌道の6つのローブのうちの同じ位相成分同士が強調されていることがわかります。高次高調波と赤外光の時間差を約1300アト秒(660アト秒の二倍)だけ変化させると、逆の位相が抽出されます。この時間差は、赤外光の周期によって決まっています。
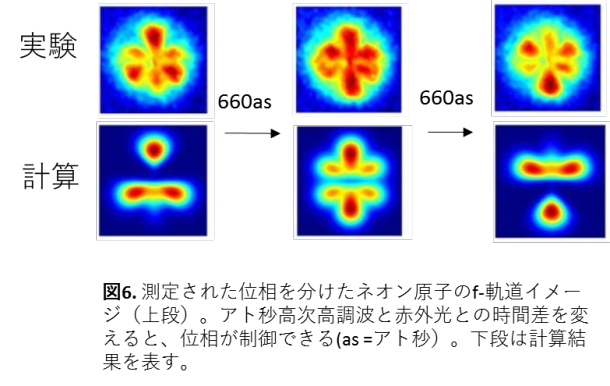
なお詳細には、13次高調波+基本波という過程だけではなく、15次高調波によって励起された状態から、1光子だけ放出するという2光子過程により、同様にf-軌道とp-軌道が生成し得ます。そこで高次高調波と赤外光の時間差の関数として測定した一連の光電子運動量分布から、それぞれの過程によって生成した異なる軌道角運動量を持つ電子波動関数の振幅と位相を完全に決定しました。その結果、f-軌道とs-軌道の寄与が大きいことがわかりました。
今後の展望
本研究では、ほぼ純粋な単一の軌道角運動量を持つ電子波動関数の密度分布(|Ψ|2)と、その位相を区別した波動関数(Ψ)に相当する分布を直接イメージングした実験結果を示しました。また、放出された光電子がどのような軌道角運動量を持つ波動関数から成っているのか、その位相と振幅を完全に決定しました(光電子の完全実験complete experimentと呼ばれます)。従来の光電子分光(光電子運動量分光法)では、イオン化により放出された光電子の分布から直接、(個々の角運動量成分を持つ)波動関数の分布を得るということは困難だったため、本研究は、アト秒時間分解・光電子分光法に対して新たな地平を開いたものといえます。
波動関数イメージングはアト秒科学における大きな目標の1つであり、今後は多電子の相関などによってどのように電子波動関数の位相と振幅が変化していくのかを、アト秒でイメージングすることなどが展望となります。また本研究で新規開発したアト秒光学系は、簡便かつ高安定でアト秒時間分解分光が可能になるので、固体や表面をターゲットにしたアト秒顕微分光法に発展できると考えられます。本研究により、ナノテクノロジーの次の世代である、電子波動関数の直接観測と制御を元にしたアト・テクノロジーの発展に繋がることが期待されます。
注:Appendix
1.波動関数:コペンハーゲン解釈によれば、ある領域の波動関数の自乗は、その領域に粒子が存在する確率を表します。波動関数は波として表現され、振幅と位相を持ちます。原子の電子波動関数はその角運動量に応じて、以下の概念図のような分布を持ちます。(色の違いは位相の違いを表します)。角運動量は電子が核からどれくらい遠くを運動しているかを表す指標で、水素型原子ではℓ=0,1,2,3という軌道角運動量量子数に応じて、s-軌道・p-軌道・d-軌道・f-軌道と呼称されます。(なおここでは連続状態の波動関数についても、軌道という用語を使用しています。)例えばヘリウム原子の電子基底状態では、2個の電子は1s軌道に収まり、ネオン原子の電子基底状態では、10個の電子はそれぞれ1s軌道に2個、2s軌道に2個、2p軌道に6個の電子が収まっています。適切な波長の光を照射すると、角運動量が1つ異なる軌道に電子が遷移(移動)します。例えば2p軌道にある電子はd-軌道かs-軌道に遷移することになります。また、それぞれの軌道角運動量に対して、2ℓ+1だけの縮退した(同じエネルギーを持つ)異なる角度分布を持つ状態があり、磁気量子数(m)で区別されます。図では、f-軌道のm=0とm=1の場合を示しています。

波動関数の「位相」の重要性について、模式的に説明すると上の図のようになります。例えば同じ位相同士の波動関数が近づくと、互いに重なり合って分子結合を作り得ますが、異なる位相同士の波動関数では打ち消しあって、結合を作らないことになります。このように波動関数の位相は、反応の選択性に大きく関係があります。波動関数の自乗、すなわち確率分布では、位相の違いは見えなくなります。
2.アト秒科学:アト秒とは時間の単位で、1アト秒は10-18秒に相当します。分子の振動(波束)運動や回転(波束)運動はそれぞれフェムト秒(10-15秒)、ピコ秒(10-12秒)の時間スケールで起こります。アト秒の科学では、原子や分子、固体表面などの内部を動く電子(波束)の運動や、イオン化に伴って放出される電子などの時間差を測定することが行われています。
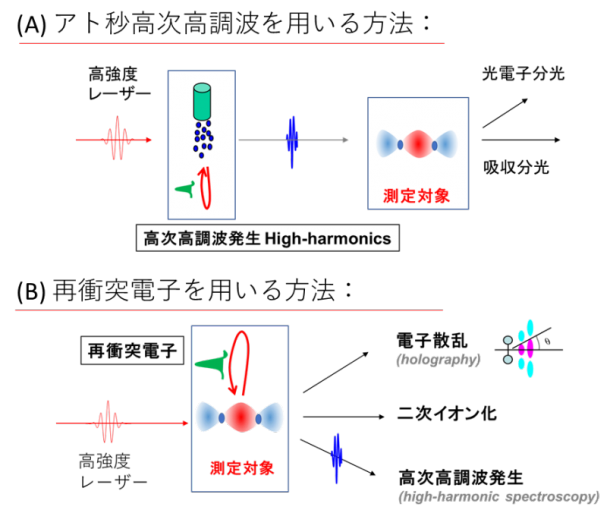
アト秒科学には主に二つの方法があります。(A)アト秒光パルス(高次高調波)をプローブ光または励起・イオン化光として試料に照射し、放出された光電子や、光の吸収を時間分解で測定する方法(P.M. Paul et al., Science 292, 1689 (2001); M. Hentschel et al, Nature 414, 509 (2001)等)、(B)再衝突する電子(アト秒再衝突電子)を用いる方法(Niikura et al., Nature 417, 917 (2002); Nature 421, 826 (2003))。再衝突電子を利用する方法では、高強度の赤外レーザーパルスを試料に照射し、放出された電子と試料との再衝突過程によって生じた散乱過程や高次高調波発生過程を調べることで、試料内部の電子運動や振動運動などを測定します。近年、固体物理にも適用されています。今回の研究は、(A)のアト秒高次高調波パルス列を励起・イオン化光として用いたものです
3.アト秒高次高調波:高強度の赤外レーザーパルス(~1014W/cm2、基本波)を、真空中に吹き出した原子や分子に照射すると、トンネルイオン化―電子再衝突過程によって、基本波(赤外光)よりもはるかに短い波長(極端紫外~軟X線領域)を持つレーザー光(高次高調波)が生成します。基本波のパルス幅が長い場合には、基本波の半周期に一回、アト秒のパルス幅を持つ高次高調波が発生し、基本波の奇数次のみを含むパルスが生じます。(例えば13次高調波では、基本波(~790nm, 1.57 eV)の13分の1の波長、エネルギーで表せば1.57eVの13倍の20.41eVになる。15次高調波は23.55 eVになる。)一方、基本波と第二次高調波をあわせて原子や分子に照射すると、奇数次と偶数次の両方が生じ、例えば13次(20.41 eV)と15次(23.55 eV)の間に14次(21.98 eV)のピークが生じます。このように、基本波の高次の奇数次や偶数次の高調波を発生することから、高次高調波と呼ばれています。

論文情報
- 掲載誌:Science
- 論文名:“Coherent Imaging of an Attosecond Electron Wave Packet”
- 著者 :D. M. Villeneuve, P. Hockett, M. J. J. Vrakking, and Hiromichi Niikura