- ニュース
- 推量問題の解析的特徴付けに成功
推量問題の解析的特徴付けに成功

- Posted
- Wed, 16 Feb 2022
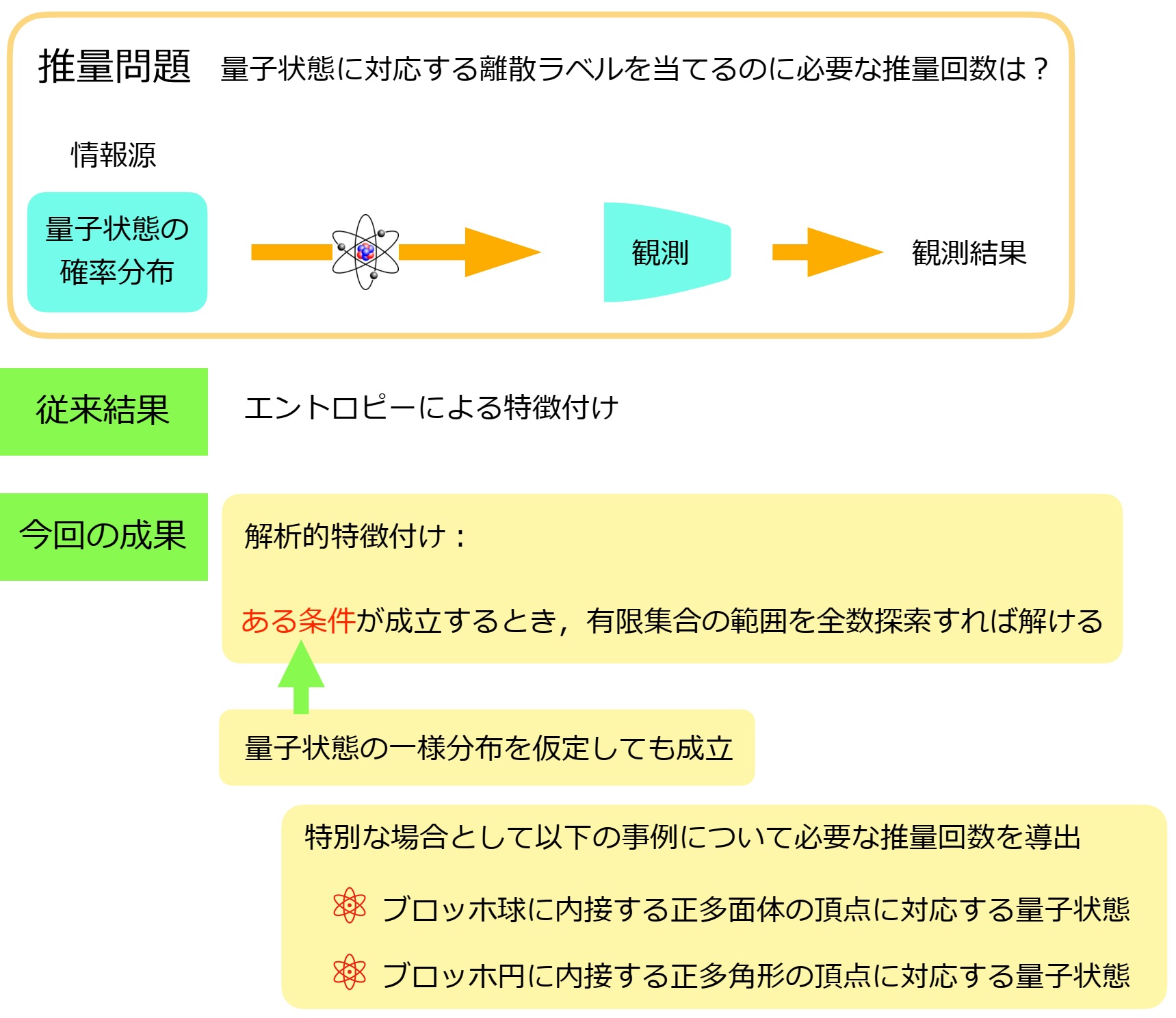
推量問題の難しさの解析的特徴付けに成功
発表のポイント
- 複数の量子状態にある、離散値ラベルの推量問題に対する難しさの解析的特徴付けに成功
- 量子状態の機械学習が求められる分野に向け、推量問題の難しさの究明につながる有効事例を示し、アルゴリズム設計の指針を与えるものと期待できる
- 量子状態の確率分布に対する、推量問題に対する研究の発展に貢献
概要
早稲田大学教育・総合科学学術院の小柴 健史(こしば たけし)教授らは、複数の量子状態にある、離散値ラベルの推量問題に対する難しさの解析的特徴付けに成功しました。複数の離散的な値がランダムに得られるという状況で、その値を推量する問題を推量問題といいますが、推量問題はさまざまな分野における基本問題であり、その推量問題の難しさの究明は重要テーマです。今回、解析的特徴付けと、その特徴付けの有効な例を示すことに成功いたしました。今回の研究による解析的アプローチは、量子AIの援用が期待できるような諸分野において、推量問題を解くためのアルゴリズム設計の指針を与えるものと期待されます。
本研究成果は、IEEE Information Theory Societyが発行する『IEEE Transactions on Information Theory』に、“Guesswork of a quantum ensemble” として、2022年1月26日(水)にオンラインで公開されました。
(1)これまでの研究で分かっていたこと
推量問題は様々な分野における基本問題であり、その推量問題の難しさの究明は重要テーマとなっていますが、情報源のランダム性はエントピー※1と呼ばれる尺度で測るのが一般的で、推量問題の難しさもエントロピーを用いた議論が中心的になっています。推量問題は、符号理論における復号問題や暗号理論における秘密鍵の安全性とも密接に関係があり精力的に研究が行われています。例えば、情報セキュリティにおける基本的技術としてパスワード利用がありますが、特定されにくいパスワードを設定することが重要です。パスワード推量問題を考えるとき、データ解析等でパスワード候補が限定された状況で、そのパスワードを特定することの難しさが議論できたりします。
物理的な現象や性質を究明するとき、データが量子状態※2の確率分布からサンプルとして抽出されることがあります。その現象や性質の究明する難しさを測ることは重要な基本課題となっています。推量するための準備としてサンプルとして得られる量子状態を観測※3し、情報を収集する必要があります。量子状態を観測すると一般的に情報が失われるため、推量問題も難しくなります。ただ、情報源が量子状態の確率分布であっても、量子状態を扱えるエントロピーが定義でき、推量問題の難しさはエントロピーで議論されています。
(2)今回の研究で新たに実現しようとしたこと、明らかになったこと
自然な言葉で定められる問題は曖昧性を持っているので、数学的な導出が可能なように適切な形式化を如何に行うかが重要です。従来の推量問題の取り扱いは、エントロピーでの議論に適した形で形式化されていますが、今回の研究においては、解析的な解を導出することを目的とし、推量問題の定式化を構成しました。エントロピーを利用した議論でも問題の難しさを明らかにすることは可能ですが、推量問題を解くために必要なアルゴリズムに対する示唆を余り与えてくれません。それに対し、解析的アプローチはアルゴリズム的な知見をもたらしてくれると期待しました。
(3)そのために新しく開発した手法
推量問題を解くために必要な最小な推量試行数の導出は、本質的に連続領域上の最適化問題になりますが、その最適化問題は解くのが一般的に「難しい問題」として知られています。ある条件を課すことにより、解空間が有限集合になることを証明し、少なくとも全数探索による解法が可能であることを示しました。特に、有限個のラベルによって規定される量子ビット上の一様分布を考えるという自然な設定は、上述した「ある条件」を満たすことを合わせて証明しました。
量子状態は数学的にはブロッホ球※4の球面上の点あるいはブロッホ円※4の円周上の点として表現されます。ブロッホ球内の正多面体の頂点(図1)あるいはブロッホ円内の正多角形の頂点(図2)をラベルとする量子状態の一様分布を考えるという例は、ある有限集合上の最適化問題を明示的に解くことによって推量問題を解くために必要な最小な推量試行数を与えることができることを例証しました。
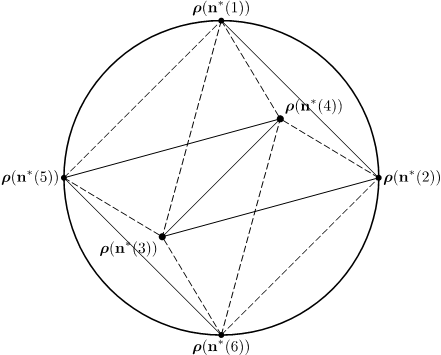
図1:ブロッホ球に内接する正8面体の例
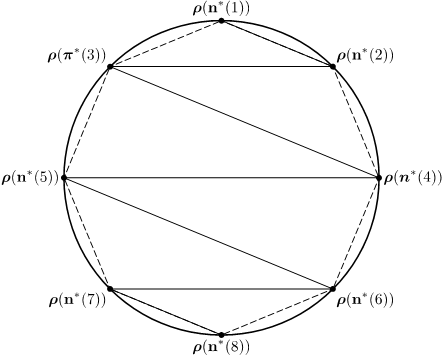
図2:ブロッホ円に内接する正8角形の場合の例
(4)研究の波及効果や社会的影響
今回の研究による解析的アプローチは推量問題を解くためのアルゴリズム設計の指針を与えるものと期待されます。実際の応用を考えた場合、さらに条件が加わり、解空間が狭くなったり特殊な形になったりするものと想定されます。課されている条件によっては最適化問題を解く効率的アルゴリズムが存在するので、そのような可能性を追究することにより実問題への応用が考えられます。
(5)今後の課題
効率的アルゴリズムが存在するような最適化問題の求解に帰着できるような推量問題に対する十分条件を与えることができたら、応用可能性に繋がります。また、量子状態の確率分布に対する推量問題に対する研究はまだまだ発展途上にあり、多面的なアプローチで取り組むことも必要かと思います。
(6)研究者からのコメント
量子コンピュータの本格的実現へ向けて研究開発が進められており、量子情報処理の可能性は、他の分野にも貢献することが認知され、例えば創薬等に繋がることが期待できる量子化学分野でも、量子情報処理を想定した研究が進められています。将来,各種データを量子状態として管理できるようになったとき、量子AIの可能性は広がります。本研究は、量子AIにつながる基本問題である推量問題に対するアルゴリズム的示唆を与える方法論を提案していることを強調しておきたい。
(7)用語解説
※1 エントロピー
ランダム性を表す尺度の一つ。情報源のエントピーが高いと推量問題は難しくなり、エントピーが低いと推量問題は易しくなる。エントピーを用いた議論は、推量問題だけでなく、ランダム性のある情報源の性質を究明するための代表的な方法。
※2 量子状態
我々が日常生活で認知される物理的に異なる複数の状態は、同時に起こることはありません。シュレディンガーの猫として有名な逸話に、箱に入っている猫が「生きている」ことと「死んでいる」ことが同時に起こりうるかという思考実験があります。原子レベルのミクロの世界では、異なる複数の状態が同時に起こることがあり、量子状態と呼ばれます。複数状態の同時重ね合わせという性質から、並行した情報処理が可能であり、量子情報処理の基本的操作となっています。これは量子コンピュータの通常のコンピュータに対する優位性として盛んに研究がなされています。
※3 観測
量子状態に対する観測は通常の物理的な状態に対する観測とは異なります。通常の物理的な状態に対する観測では、例えば温度や位置が観測により一意に決定され、観測行為は物理的な状態に影響を与えません。量子状態に対する観測により得られる情報は一意には決まらず確率的であり、観測によって得られた情報に応じて量子状態は別の量子状態へと変化します。
※4 ブロッホ球とブロッホ円
通常のコンピュータの情報の単位である1ビットに対応する量子状態を、1キュービットと呼びます。1キュービットの量子状態は、ビット0とビット1を重ね合わせた状態を取ることができます。数学的には1キュービットは複素数を要素とする2次元ベクトルとして表現します。また、1つの複素数は2次元の実数で表現できることを考えると、1キュービットは4次元実数ベクトルで表されます。ただ、ある2次元複素数ベクトルで表現される量子状態と、そのベクトルを大きさ1の複素数倍を乗じてえられる2次元複素数ベクトルは観測では識別できず、同じ状態として認識されます。同じ状態として認識される量子状態を同値なもとの考えると、1キュービットの量子状態全体は3次元実数の単位球の表面全体と1対1の対応関係があり、その単位球をブロッホ球といいます。また、量子状態全体は、表現は難しく、ブロッホ球を2次元に制限したものをブロッホ円といいます。
(8)論文情報
雑誌名:IEEE Transactions on Information Theory
論文名:Guesswork of a quantum ensemble
執筆者名(所属機関名):Michele Dall’Arno(京都大学、早稲田大学)、 Francesco Buscemi(名古屋大学)、Takeshi Koshiba(早稲田大学)
オンライン掲載日時:2022年1月26日(水)
掲載URL:https://ieeexplore.ieee.org/document/9693515
DOI:10.1109/TIT.2022.3146463