量子インスパイアード技術を用いた大量データのクラスタリング手法の開発
多様な分野における画像を含む時系列データの分析に利用
発表のポイント
- 科学、工学、環境、農業、生命科学、経済学をはじめ多くの分野で、時間とともに変化するデータ(時系列データ)を大量に収集し、類似度に応じて適切にグループ分け(クラスタリング)し、特徴的な挙動を解析することが重要となっています。
- 本研究では、時系列データのクラスタリングを組合せ最適化問題として捉え、この問題に特化した量子インスパイアード技術を適用することで、大量なデータのクラスタリングを高速に行うことに成功しました。
- 外れ値を考慮しつつ所望のクラスタリングを行う新たな方法を提案し、大きなノイズを含む画像データにおいて高い精度のクラスタリングを行うことができることを実証しました。
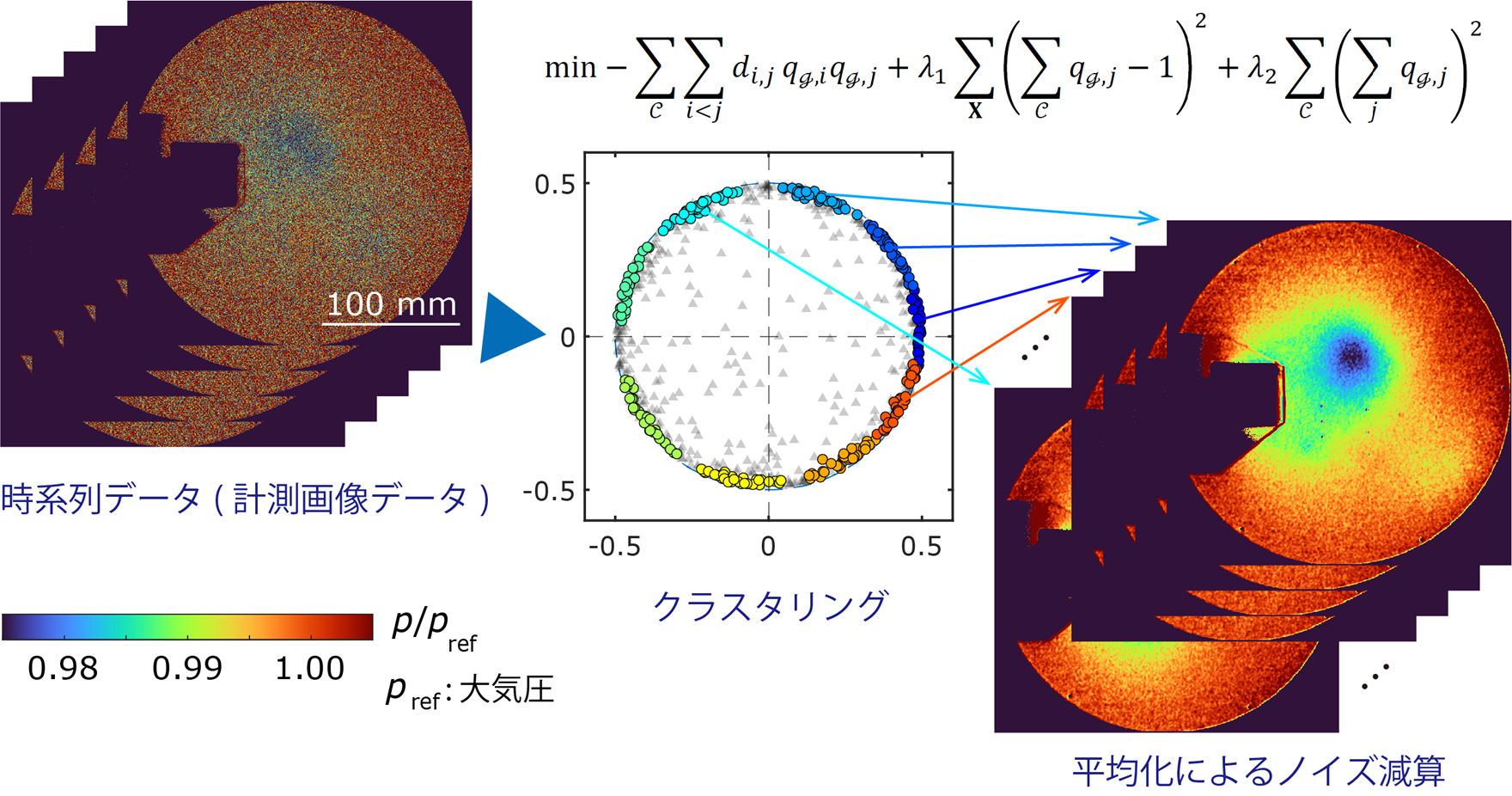
図1:本研究による高精度クラスタリング結果
研究概要
早稲田大学理工学術院教授 松田佑(まつだゆう)、同大学院生 井上智輝(いのうえともき)、窪田航陽(くぼたこうよう)、東北大学流体科学研究所教授 永井大樹(ながいひろき)、同助教 伊神翼(いかみつばさ)、愛知工業大学工学部教授 江上泰広(えがみやすひろ)らの研究グループ(以下、「本研究グループ」とする)は、大きなサイズで大量の時系列データ*1のクラスタリング*2を組合せ最適化問題*3として捉え、これに特化した計算技術を応用して高速な計算を可能としました。また、どのクラスタにも相応しくない外れ値を、クラスタに含まないようなアルゴリズム構築を行いました。これにより、多分野での画像を含む時系列データの解析に本手法が貢献できると期待されます。
このたびの成果は、英国の科学雑誌Natureが運営するオープンアクセスジャーナル『Communications Engineering』に、“Clustering Method for Time-Series Images Using Quantum-Inspired Digital Annealer Technology”として、2024年1月10日(現地時間)に掲載されました。
今回の研究の背景・課題
科学、工学、環境、農業、生命科学、経済学をはじめとして非常に多くの分野において、時系列データが収集されています。複雑な挙動を示す多くのデータを適切にクラスタリングし、特徴的な挙動を抽出し解析することが、複雑な現象への理解を深めるための非常に重要なプロセスと認識されています。
このような時系列データのクラスタリングを行う方法は「時系列クラスタリング」と総称され非常に盛んに研究が行われています。近年では、データストレージの大容量化やセンサ性能の向上が劇的に進み、また画像データを扱うことも増えており、大きなサイズのデータが大量に得られるようになりました。そのため、このようなデータの巨大な集合を高速にクラスタリングすることが必要になっています。
今回の研究で新たに実現したこと
一般に時系列クラスタリングでは時系列データの集合の中から、互いのデータの類似度を計算し、その類似度に応じてデータをクラスタリングします。すなわち、類似度の高い似通ったデータをひとまとまりのクラスタとして、類似度が低く似ていないデータと区別していきます。
データサイズが大きくなり、データ数も大量になると、このクラスタリングの計算に時間がかかります。クラスタリングは組合せ最適化問題のひとつと考えることができるため、組合せ最適化問題に特化した量子コンピュータなどで注目度の高い新しい計算技術が活用でき、高速な計算が可能です。一方で、クラスタリングを行う際には、しばしばどのクラスタにも相応しくないデータ(外れ値)も出てきます。このような外れ値をクラスタに含まないようなアルゴリズムを開発しました。
新しく開発した手法
本研究グループは、
- 各クラスタに入るデータ間の類似度の和が大きくなる
- 1つのデータは最大1つのクラスタに入る
- 各クラスタに入るデータ数とその分散を調整する
という3つの制約を課すクラスタリング方法(以下、「本手法」とする)を開発しました。
条件①は、互いに似通ったデータを同じクラスタに入れるための条件です。条件②は1つのデータが複数のクラスタに入っていると解析において不都合となる場合が多いので、これを避けるための条件になっています。条件③は、クラスタに含まれるデータ数と分散を調整します。これによって各クラスタの大きさを調整します。例えばクラスタに含まれるデータ数を多く設定すれば、外れ値をクラスタに含みやすくなります。逆にクラスタに含まれるデータ数を少なくすれば、外れ値をクラスタに含まなくなります。なお、これらの3つの条件の重みを変えることで、例えば同頻度で各クラスタに該当する現象が生じていると予想される場合に、各クラスタに入るデータ数を揃えることもできます。本研究ではこの例として、周期的な時系列データに対して本手法を適用しています。
本手法は、条件に合うようなデータの組合せを考える組合せ最適化問題となっています。本研究グループは、この組合せ最適化問題を解くために、Fujitsu Computing as a Serviceの構成技術のひとつで組合せ最適化問題の計算に特化した新しい計算技術であるComputing as a Service Digital Annealer (以下、「富士通デジタルアニーラ」*4とする)を利用しました。
研究の成果
本手法が最も有効と考えられる周期的な変化を示す画像データに対し、従来の計算技術を利用した既存手法による結果との比較を行いました。定期的にある現象が繰り返される周期現象は非常に多くの分野においてみられる現象で典型的な時系列データのひとつです。
本研究ではこのような周期現象に着目し、著者らが以前の論文1-3において計測した画像データのクラスタリングを行いました(図2)。この画像データは流れに直角に置かれた角柱後方にできるカルマン渦*5を感圧塗料法*6によって計測したもので、周期的に渦が発生し流れていきます。カルマン渦は、工学だけでなく気象学においても頻繁にみられる重要度の高い現象です。ただし非常に大きなノイズが含まれています(図2a)。このようなノイズを多く含む周期現象のデータは、1周期を複数の位相に分割して、同一の位相帯に相当する画像データを集めて平均化することでノイズの影響を低減したデータを得るというニーズがあります。これは、周期現象をタイミング毎のクラスタにクラスタリングし、各クラスタ内でデータを平均化することに相当します。しかし、実際に計測されるカルマン渦は、著者らの以前の研究で示されているとおり、周期から外れて渦が発生するなど外れ値も多く発生します。そこで、外れ値を含まないようにクラスタを形成する必要があります。また周期現象なので各クラスタに入るデータ数は同程度になると期待されますので、この点も考慮しなくてはなりません。
クラスタリングを行った結果が図3です。この図では、各データをその類似度に応じて多次元尺度構成法*7によって平面上にプロットしています。似通ったデータは近くにプロットされており、今回ターゲットとしている周期現象は外周の円上にプロットされたデータとなります。円の内側にプロットされたデータは、外れ値とみなせます。このため、グラフにある円上のデータのみを複数のグループに分けるクラスタリングが期待されることになります。既存手法のひとつであるk-means++法*8を用いてクラスタリングを行った結果では、外れ値がクラスタに含まれており、また各クラスタも互いに重なりが見られます。加えて、conditional image sampling (CIS) 法*9と呼ばれる感圧塗料計測法に特化した手法を用いた結果では、外れ値をいくらか考慮することができていますが、十分には除ききれていないことが分かります。またやはりクラスタ同士に重なりが生じています。これに対して、本手法では外れ値を除きつつ、クラスタも重なりがなく、望んだとおりにクラスタリングできていることが分かります。
図4は各クラスタ内でデータを平均化することで得られた圧力分布を表します。元のデータは図1の左のように非常に大きなノイズを含みますが、平均化することで大幅にノイズを削減することに成功し、カルマン渦が明瞭に可視化されています。またこの図は大気圧で除した値を示していますが、圧力の変化は数%と非常に小さいことも分かります。本手法では、大きなノイズを含んだ数%の信号変化のデータから、外れ値を考慮しながら上手くクラスタリングができることを示しています。
また一般的なデータに対する性能を確認するために、オンライン公開されているデータセットに対するクラスタリングを行いました。その結果、本手法が既存手法と同程度の結果を与えることを確認しました。このデータは、人工衛星で観測された土地利用の時系列データであり、本手法が流体計測データに留まらず利用できることを示しています。
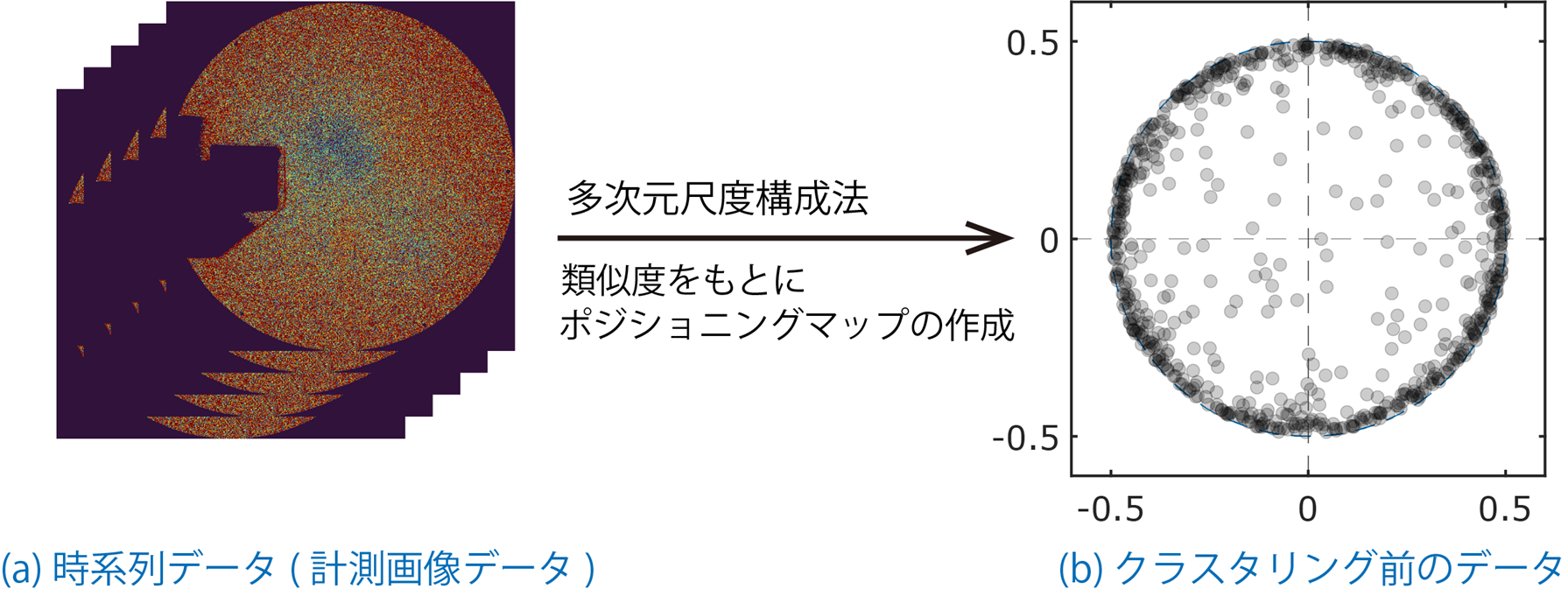
図2:本手法の有効性を確認するために検証した画像データ
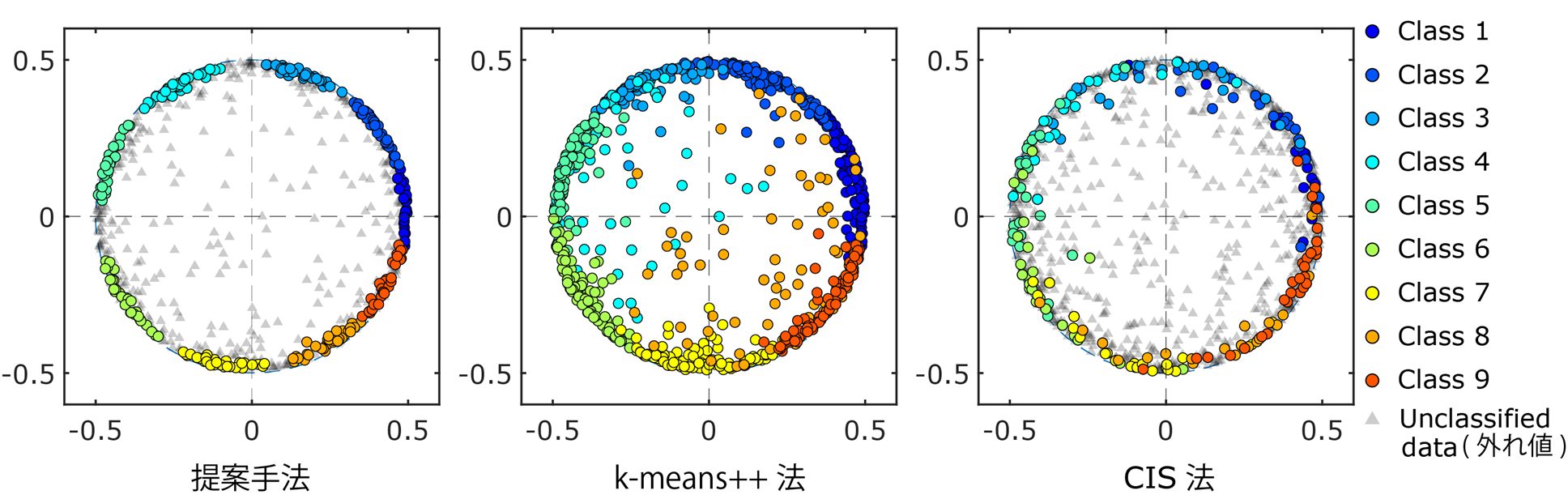
図3:本手法、及び既存手法によるクラスタリング結果
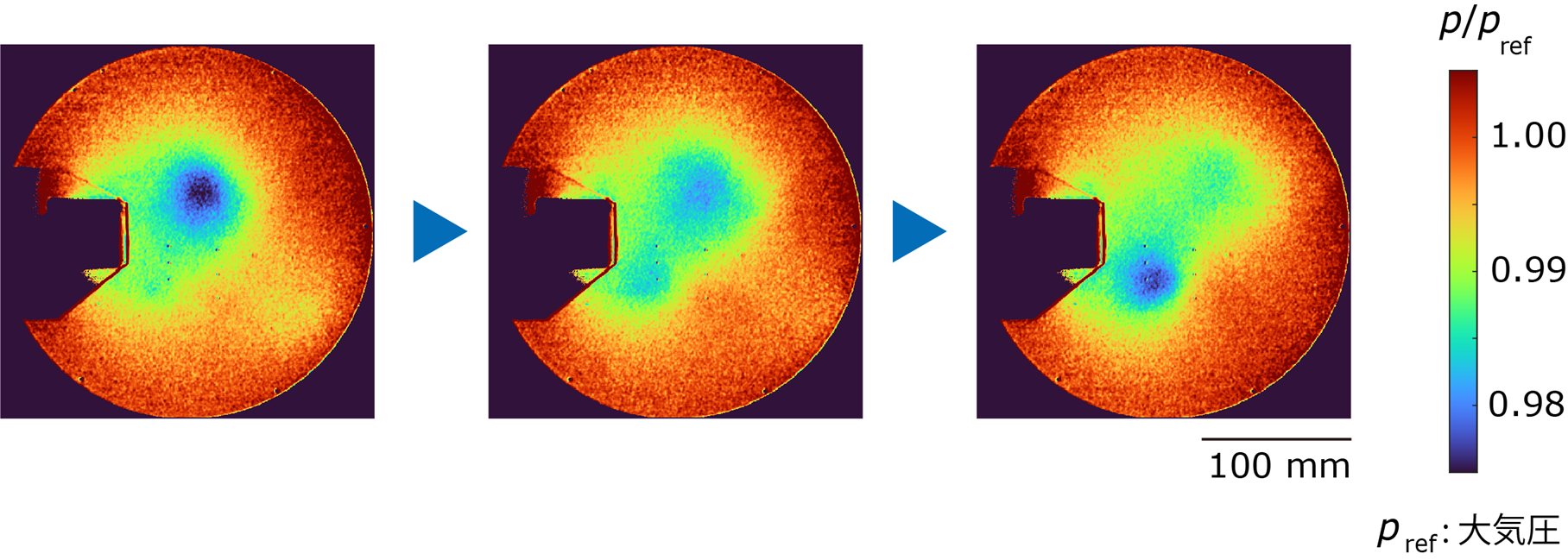
図4:本手法のクラスタでの平均化結果例。位相順に並べた渦の流れの例。
研究の波及効果や社会的影響
時系列データは非常に多くの分野で用いられています。今回は流体計測画像を例としてクラスタリング例を実証しました。このデータは非常に大きなノイズを含んでいますが、本手法で上手くクラスタリングできることを示しました。このようなケースは流体計測に限らず他の分野でも多くあると考えられます。今回発表した論文においては、本手法は基礎的な内容となっていますが、その分、気象、生命科学、経済をはじめとして応用分野が広いと考えています。また近年では、新しいコンピューティング技術の開発が活発に行われております。これらのコンピューティング技術を広い分野の研究に活用するという視点からもインパクトが大きいといえます。
研究者のコメント
今後、計測によって得られる時系列データは増加の一途をたどると考えられ、これらを上手く解析することが重要となります。時系列クラスタリングは富士通デジタルアニーラのように組合せ最適化問題に特化した計算技術を有効に利用できる分野であり、各専門分野での解析に活用いただければ幸甚です。
用語説明
※1 時系列データ
時間と共に変化する量についてのデータ。例えば、気温の時間変化、株価や為替相場など。
※2 クラスタリング
データを類似度に応じてグループ分けすること。教師なしの機械学習のひとつ。教師あり学習である「分類」とは異なる。作られたグループはクラスタと呼ばれる。また類似度とは2つのデータがお互いにどれだけ似ているのかを示す指標。
※3 組合せ最適化問題
考えられる組合せの中から、与えられた条件を満たす最適な組合せを選ぶ問題。巡回セールスマン問題やナップサック問題などがよく知られている。
※4 富士通デジタルアニーラ
富士通株式会社がサービス提供している、量子現象に着想を得たコンピューティング技術で、組合せ最適化問題を高速に解く技術。
https://www.fujitsu.com/jp/digitalannealer/index.html
※5 カルマン渦
流れの中に角柱や円柱を置いたときに、これらの物体の後方で見られる特徴的な渦。角柱、円柱の両端から交互に渦が出ているように見える。カルマン渦は、一定時間間隔で同じ現象が繰り返し生じる周期現象のひとつ。
※6 感圧塗料法
感圧塗料は、一般に酸素消光作用を有するりん光分子とこれを模型表面に保持固定するためのバインダから構成される。感圧塗料法では、このりん光分子の放つ発光の強度が圧力に応じて変化することから、感圧塗料の発光強度分布を計測することで圧力分布を計測する。
※7 多次元尺度構成法
データが似ているかどうかを視覚的に分かりやすくポジショニングマップとして表す手法。似通ったデータが近くにプロットされる。
※8 k-means++法
k-means法の問題点を改良した手法。k-means法とは、最初に適当にクラスタの中心点を設定してクラスタを決定する。クラスタに含まれるデータの平均値を算出し、その点を新たな中心点としてクラスタを修正する。この作業をクラスタが変化しなくなるまで続ける手法がk-means法。この方法では、最初に設定した点によって結果が変わる恐れがある。これを修正したのがk-means++法。
※9 conditional image sampling (CIS) 法
感圧塗料計測法におけるクラスタリングに特化して使用されている手法。この手法では、別途、半導体圧力センサを用いて、周期現象を捉え、その情報をもとに画像をクラスタリングする。圧力場全体を計測してクラスタリングするわけではないので、半導体圧力センサで計測できない箇所の渦の乱れを考慮することができない。
論文情報
雑誌名:Communications Engineering
論文タイトル:Clustering Method for Time-Series Images Using Quantum-Inspired Digital Annealer Technology
著者:井上智輝(早稲田大)、窪田航陽(早稲田大)、伊神翼(東北大)、江上泰広(愛知工業大)、永井大樹(東北大)、柏川貴弘(富士通)、木村浩一(富士通)、松田佑(早稲田大)
掲載日時(現地時間):2024年1年10日(水)
DOI: 10.1038/s44172-023-00158-0
URL:https://doi.org/10.1038/s44172-023-00158-0
参考文献
1 Egami, Y., Hasegawa, A., Matsuda, Y., Ikami, T. & Nagai, H. Ruthenium-based fast-responding pressure-sensitive paint for measuring small pressure fluctuation in low-speed flow field. Meas. Sci. Technol. 32 (2021). https://doi.org/10.1088/1361-6501/abb916
2 Inoue, T., Matsuda, Y., Ikami, T., Nonomura, T., Egami, Y. & Nagai, H. Data-driven approach for noise reduction in pressure-sensitive paint data based on modal expansion and time-series data at optimally placed points. Phys. Fluids 33 (2021). https://doi.org/10.1063/5.0049071
3 Inoue, T., Ikami, T., Egami, Y., Nagai, H., Naganuma, Y., Kimura, K. & Matsuda, Y. Data-driven optimal sensor placement for high-dimensional system using annealing machine. Mechanical Systems and Signal Processing 188 (2023). https://doi.org/10.1016/j.ymssp.2022.109957









