
- 小林正人(Masato Kobayashi)助教(2012年7月当時)
量子化学計算とは
自然科学で扱う様々な現象について、理論モデルを立てて計算をすることにより、その原理を探り、また予測を行う学問を計算科学と言います。私が計算科学と出会ったのは高校生の時でした。もともとコンピュータが好きだったこともあるのですが、実験で見られるような現象が、どのようにして起こるのかを計算で明らかにするというのがとてもおもしろく感じられました。その後、大学に入って化学現象は電子や原子核レベルの非常に小さな世界の理論で説明されると知り、これを専門に研究する量子化学という学問の大切さを実感しました。
こうして私は量子化学計算の研究を始めたわけです。化学反応を起こす「分子」はいくつもの原子からなり、原子は原子核とそれを取り巻く多数の電子からできています。多くの化学反応は電子が動くことによって起こります。ということは、化学反応が起こる仕組みを明らかにするには、分子の中の電子の状態を知らなければならないということです。電子の状態は、シュレーディンガー方程式という方程式を解くことによって求められます。この方程式を、コンピュータを使って数値的に解くのが量子化学計算です。
シュレーディンガー方程式を解くと、分子の中の電子分布を表す「波動関数」と、分子の安定度を表すエネルギーが得られます。これらがわかると、その分子がどのくらい反応を起こしやすいのか、またどの部分で反応が起きるのか、といったことがわかるのです。
大規模分子の計算の難しさ
化学現象を理論的に扱うためにはシュレーディンガー方程式を解けばよい、ということはわかりましたが、実はこれには大きな問題があります。それは、シュレーディンガー方程式を解こうとすると、多体問題と呼ばれる問題に直面してしまい、厳密に解くことは一般的には不可能だということです。ですから、量子化学計算ではシュレーディンガー方程式を実際に解ける形に近似した理論を用います。それでもなお、量子化学計算の計算量は莫大であるため、スーパーコンピュータを利用することもしばしばです。
スーパーコンピュータと言えば、日本には、世界第2位の計算能力を持つスーパーコンピュータ「京」があります。「京」はみなさんの持っている最新のパソコンのおよそ10万倍の計算が可能ですから、「『京』を使えば、計算量がどんなに増えても大丈夫」と思う方もいるかもしれません。しかし、話はそう簡単ではないのです。下の表に量子化学計算で用いられる代表的な近似方法と計算時間を示しました。計算量は分子の大きさが大きくなると急激に増加してしまうことがわかります。表の一番下には、1000倍の計算量の計算機を利用したときに元よりもどれだけ大きな分子が計算ができるかを示しましたが、最も簡単なHF法でもたった10倍にしかなりません。さらに、近似の精度を高めて、より正確な解が得られるように選択すると、たとえスーパーコンピュータを使っても、計算できる分子の大きさはほとんど変わらないのです。そこで、量子化学計算の研究者は、計算量をなるべく少なく抑えて大きな分子を精度よく計算するための計算法を研究しています。近似の方法を工夫して計算量を減らしながらも、精度を高く保とうという試みです。
 (※) O(Nn);計算時間が原子数(N)のn乗に比例して増えることを示す。nが大きいほど急激に増える。
(※) O(Nn);計算時間が原子数(N)のn乗に比例して増えることを示す。nが大きいほど急激に増える。
表:分子の大きさ、計算精度と計算時間の関係(提供/小林正人助教)
困難は分割せよ
私は、分子全体を直接計算するのではなく、分割した小部分(部分系)の計算をする分割統治法(Divide and Conquer法; DC法)に注目しました。DC法では、まずそれぞれの部分系についてシュレーディンガー方程式を解いて波動関数を求めます。そして、それらを統合して全体の分子の電子密度を計算します(図)。この方法であれば、小さな部分系についての方程式をとけばよいので、計算時間が大幅に短縮されます。
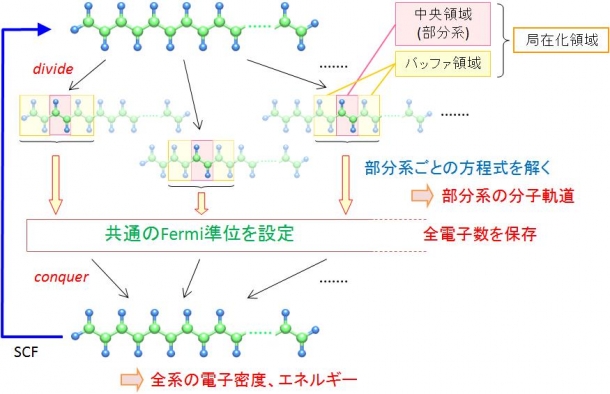
図:分割統治法の概念
DC法で最も重要なポイントは部分系の周辺に「バッファ領域」を定めるということです。注目する部分系の周りを少し余分に取り出して波動関数を求めることで、切り出しによる誤差を小さく抑えるためです。その後、バッファ領域の部分で重複がないように工夫して足し合わせることで、分子全体の電子密度を定めます。バッファ領域を大きくとるとそれだけ計算量は増えますが、高精度の計算が可能になります。
よりリアルな近似への挑戦と発見
DC法によって計算の高速化ができることはわかりました。ただし、ここまでお話してきたのは低精度の一体近似理論HF法への適用を前提としたものです。この方法では、電子を粒子ではなくもやっとした雲のような分布と仮定して、電子についての波動関数を求めます。しかし、すでに述べたようにこれは精度の低い近似であり、シュレーディンガー方程式のよりよい解を得るには、2つの電子の粒の間にあらわに働く相互作用、「電子相関」を考慮した理論(表1の右3つの計算法)を用いなくてはなりません。
そこで私が挑戦したのは電子相関を考慮したDC法の確立です。詳しくは述べませんが、エネルギー密度解析(EDA)という方法を用いて、電子相関を考慮したより高精度な計算を可能にしました。この計算法は現在、GAMESSという世界で広く使われているフリーの量子化学計算ソフトウェアに組み込まれています。
量子化学計算を使って
私はあくまでも新しい材料の開発を中心とした応用に興味があります。例えば、電気伝導性の高い有機材料は現在電子機器の部品として大きな需要がありますが、そうした材料も計算を使って「なぜ電気伝導性が高いのか」を知ることが出来ればさらによい材料の開発につながります。 私は「京」の戦略分野の一つに加わっており、こうした開発に「京」を役立てるため、研究を進めています。私の研究が量子化学計算だけでなく、広く化学の発展に少しでも貢献できればと思います。
取材・構成:青山聖子/高田成海
協力:早稲田大学大学院政治学研究科J-School










