
A desire to grasp the essence of mathematical thinking
Since childhood, I have always been mathematically inclined, although I never enjoyed memorizing equations. It seemed pointless to me to memorize such an equation that follows immediately from the definition. In addition, deriving a solution using a memorized equation did not feel like an accomplishment to me. I realized that it was only when I understood the concept that the argument expresses and the inference behind its proof that I felt accomplished and that I had gained an understanding of it and I still feel the same way today.
Somehow, I developed a belief that for every mathematical argument, there must be a strict proof and this belief became a strong conviction when I met my high school math teacher who always gave clear and precise answers to all my demanding questions. I joined the mathematics department at university because I wanted to truly understand mathematics. However, I ran into a massive wall in the form of seemingly incomprehensible mathematical proofs when faced with highly abstract and esoteric university mathematics. At this time, I found a subject so-called “proof theory” in a research field called “foundations of mathematics”. Thought I didn’t know the actual research of proof theory at all, I thought I might overcome my wall by studying such a kind of subject dealing with mathematical proofs, and I began studying foundations of mathematics intensely. My struggle from this time led to my present research topic as “a desire to grasp the essence of mathematical thinking”.
Foundations of mathematics – analyzing mathematics with mathematics
Mathematics is often classified into the subgroups; Analysis, Algebra, Geometry, and others. My field of expertise, Foundations of Mathematics, would fall into the subgroup “others” as it considered an “eccentric” branch of mathematics. Analysis, Algebra, and Geometry are mathematics dealing respectively with real numbers, figures, and algebraic structures etc., but Foundations of Mathematics deals with mathematics itself, which is possible via crucial methodology called “formalization”.
Brouwer’s intuitionism and constructive mathematics
Since the time that contradictions in simple set theory were discovered, problems associated with foundations of mathematics became important problems for pioneering mathematicians. In the early 20th century, a Dutch topologist Brouwer argued that mathematics is a mental product by mathematicians, and any existence in mathematical proofs must be shown by constructing the witness. To oppose Hilbert’s formalism, he attempted to reconstruct mathematics based on a unique philosophy called “intuitionism”. Brouwer’s mathematics was not accepted by mathematicians at that time, but “intuitionistic logic” introduced by Brouwer’s disciple, Heyting, to formalize constructive reasoning in Brouwer’s mathematics, had notable impact on the development of foundations of mathematics and computer science afterward.
Constructive mathematics developed by Bishop and others since the 1960s is (limited) mathematics that only allows constructive reasoning for its proofs. Presently, it is considered to be mathematics based on “intuitionistic logic”. For example, in constructive mathematics, the law of the excluded middle—“all propositions are either true or false”— which is an implicit supposition in mainstream mathematics, is not accepted as universally valid principles. In constructive mathematics, “proposition P is true or proposition P is false” means “there is a constructive proof that ‘proposition P is true’” or “there is a constructive proof that ‘proposition P is false’”. Of course, however, we do not have a proof for either of these for ALL propositions (at least not at this point). For example, we do not have a proof for either of its truth or its falsity for unsolved mathematical problems such as the Riemann hypothesis or the P versus NP problem.
Hilbert’s formalism and reverse mathematics
In the early 20th century, a pioneering mathematician, Hilbert, attempted to show consistency in past mathematics while preserving the law of the excluded middle. For that reason, he formalized mathematical arguments as logical formulas consisting of a small number of logical symbols and mathematical reasoning used for proofs as manipulation (inference) rules for formulas, and try to show the formal system, which is identified with mathematics, does not derive a contradiction, through an elementary way based on finitistic standpoint. This attempt by Hilbert is known as Hilbert’s program. According to Gödel’s incompleteness theorems, Hilbert’s program was revealed to be impossible. But Hilbert’s methodology of “formalizing mathematical theory and analyzing formalized subjects”, which is called “formalism”, was passed on as the standard methodology in foundations of mathematics.
Subsequently, a research program called reverse mathematics has been developed since the 1970s. In reverse mathematics, one formalizes various mathematical theorems on an appropriate base system, and examines the minimum axioms for proving each theorem. The selection of the base system is extremely important since it reflects “the standpoint from which mathematical theorems are analyzed”. Traditional reverse mathematics employs a base system called RCA0 that corresponds to computable mathematics. This can be summarized as “how much of the existence of incomputable sets must be needed to prove various mathematical theorems?”. In recent years, some intuitionistic version of reverse mathematics, in which the base system RCA0 is replaced by its intuitionistic fragment where the inference rule is weakened from “classical logic” that formalizes reasoning for proofs in ordinary mathematics to “intuitionistic logic” described earlier, has been carried out.
My current research interest is in constructivism in mathematics, and I would like to develop reverse mathematical analysis on mathematical thinking based on constructive reasoning. Constructivity is a common characteristic between many mathematical proofs, and for me, it seems to be associated with the essence of mathematical thinking. To that end, a base system that is suitable for such analysis must be constructed.
Is intuitionistic logic really a formalization of constitutive reasoning in mathematics?
Intuitionistic logic is strictly weaker logic compared to classical logic, and it is known that when the law of excluded middle discussed above is added to intuitionistic logic as an axiom, classical logic can be obtained. Therefore, presently, it is generally understood that “intuitionistic logic is classical logic minus the law of the excluded middle”. However, why can “constitutive reasoning” be obtained by simply removing the law of excluded middle from classical logic corresponding to “ordinary mathematical reasoning”? Is constitutive reasoning completely formalized by intuitionistic logic? Actually, it is not an overstatement to say that the idea that intuitionistic logic corresponds to constructive reasoning is an almost common understanding even by researchers of foundations of mathematics. However, it is just because of the empirical fact that the proofs in constructive mathematics can be simulated over a base system based on the intuitionistic logic known, and the theoretical basis for intuitionistic logic being the exact formalization of constitutive reasoning remains insufficient. Moreover, there is a known logical principle which is not provable in intuitionistic logic but can be though of as constitutive in some sense. This fundamental problem with formalization of constitutive reasoning does not have a definitive answer since intuitionistic logic was proposed in the 1920–1930s and holds until today, and has been studied continuously to this date from both aspects of philosophy and mathematics.
I would like to provide some mathematical answers to this philosophical question, and am running several studies simultaneously from different aspects. To further examine this problem, I actively communicate with experts of the subject called philosophy of mathematics. Though there is still much to do, I hope that one day, I can conduct a study on the essence of mathematical thinking through mathematics.
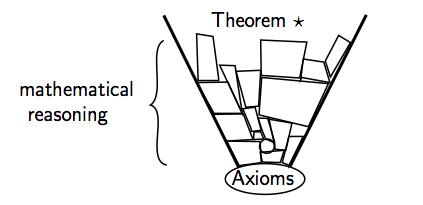
Figure: Image of the structure of mathematics
In cooperation with: Waseda University Graduate School of Political Science J-School










