
- Noboru Ito, Assistant Professor(January, 2014)
Knots
Suppose that when you are doing something like sewing, there is a length of thread or string before you that has become arranged in a complex manner as shown in the left side of Figure 1. Can this string be untangled to become like the right side of the figure? I believe it is quite difficult to make a conclusion just from looking at it. Similar to how everyone, including myself, struggled with the question “Just who am I?” during their adolescence, there are cases that arise where even if one is present in a situation, can look at its actual conditions, and can even handle the object of a problem with one’s own hands, it is still not an easy task to fully comprehend it.
It is my personal goal to solve the problem posed by the difficulty of bridging gaps that exist between intuition and understanding as described above, and to do so through the use of knots, a representative tool in the understanding of spatial perception.

Figure 1: String that has become tangled in a complex manner, and string that has been untangled
Research Procedures Involving Knots
So then, how can we make a distinction involving a complex knot like in the example? The methods to do so can be classified into the following two points.
Ⅰ.Prove that 2 knots are different
Ⅱ.Prove that 2 knots are identical
First, let me explain the concept of point I. Suppose that you see before you a rubber ball and a one-person life preserver. What makes us aware that these two objects are different from each other? For example, if we compare the number of holes in the rubber ball and in the life preserver, one has zero holes, while the other has one. We can use the two mathematical principles of “creating an equivalence between a shape and a number” and “the idea that zero and one are different numbers” to distinguish between their shapes. We also can use a similar technique in making distinctions for knots. In modern mathematics, systems to create equivalences between shapes and numbers are known as “invariants”. Over this year and the last, I have proceeded with research to create new invariants for shapes, which I will give examples of later.
Next, allow me to explain the procedure used for II. If the processes for transforming one knot into another fall among 3 types of local string moves (Figure 2, top row), then the two knots can be considered to be the same. In other words, if the processes for transforming one knot into the other are broken down and expressed individually, and the 3 types of transformation cases can be found to apply to them, then it can be proven conclusively that the two knots are identical. In the case of Figure 1, if the 3 types of transformations are correctly applied in succession to the left knot, it is possible to arrive at the untangled figure shown to the right.

Figure 2: Three types of local transformations for knots (top row), the local transformations for their corresponding shadows (middle row), and the two types of RIII moves (bottom row, dotted lines represent the state of their connections)
Let us now look only at the shadows of these knots. All of their shadows can become circles by applying the 3 types of transformations shown in the middle row of Figure 2. Now, even if the moves applied to the shadows are restricted, can we successfully understand the movements of those knot shadows? Let us consider 3 cases.
・Case 1: Prohibit RI moves only.
・Case 2: Prohibit RII moves only.
・Case 3: Prohibit RIII moves only.
Case 1 has actually already been solved, in the year 1937. Case 2, however, is still largely unsolved even by modern, leading-edge research. In my studies, I attempted to divide RIII into 2 types (wRIII and sRIII) and in cooperation with Koki Taniyama (Professor, School of Education, Waseda University) and Yusuke Takimura (2nd-year Master’s Student, School of Education, Waseda University), we partially solved problems for both types. As a result, I was able to discover a quantity X(P) where the remainder of division by 3 for the transformation using RI and sRIII (named strong(1, 3)) is an invariant. Also, a complete solution for Case 3 has been provided in a joint paper (published in 2014) by Mr. Takimura and myself.
My participation in a Japan-Germany cooperative graduate school program (Japan coordinator: Yoshihiro Shibata [Professor, School of Fundamental Science and Engineering, Waseda University]) gave me the opportunity to present lectures overseas from 2009. While doing so, in 2010 I had the good fortune to become acquainted with the distinguished mathematician Oleg Viro (Professor, Stony Brook University), and was able to receive advice from him. After more than 3 years since then, I have finally begun to glimpse the initial footholds to the “homework” I received from Professor Viro when we first met.
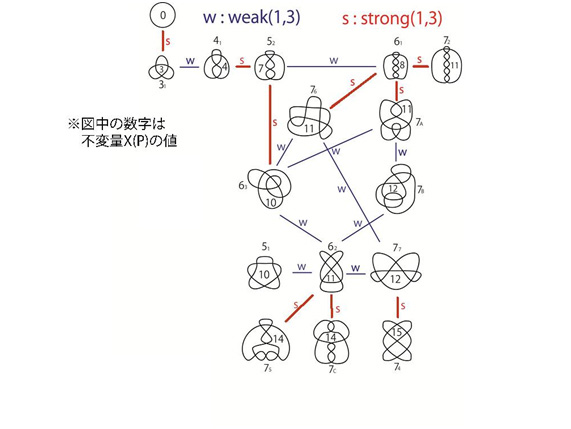
Figure 3: It can be seen that for the transformations indicated by the red lines, X(P)(mod 3) in the diagram is invariant.
The Thinking of a Mathematician
I am always thinking about 3 or 4 mathematical problems in my mind. These have different levels, from unsolved questions that seem like they could be settled in a year or so, to large-scale problems requiring many tens of years to unravel. Of course, the “homework” from Professor Viro is included in these.
In addition, I also set aside several hours every day to think about nothing but mathematics. This is a rule that Katsuya Eda of Waseda University (Professor, School of Fundamental Science and Engineering, Waseda University) tells his students to follow as mathematics undergraduates, with the premise of “at least 3 hours every day”. I have since recognized 3 hours to be the minimum level for this to be effective, and have continued to follow this practice without fail ever since my time as an undergraduate. According to Professor Eda, “‘Every day’ means every single day”, meaning that it must be done every day rigorously, regardless of whether the day is o-bon, New Year’s Day, or a weekend. Continuing to do so will enable one to accomplish many things. Over time, even mathematical concepts that at first seem nearly impossible to grasp will slowly ingrain themselves into your mind. Furthermore, one will become able to think about even multiple-stage proofs while just taking a leisurely stroll. Ultimately, at some time on some day, there will be an instant when you will realize that you have solved your problem. If you make efforts to keep a problem close at hand and always in mind, there are some whose answers will arrive in a completely natural way.
How is Knot Theory Useful?
Since the age of Gauss, knot theory has had a connection to the study of electromagnetism, and subsequently it and the field of physics have had mutual effects on each other. In particular, since the 1980s, theories on “quantum invariants” which have a physical background have been greatly developed by mathematics and physics. When considering quantum field theories and quantum invariants, the traces left by moving particles as they fly about (= lifespans of those particles) are viewed as knots. Looking even further, the role of knot theory as related to string theory has also recently been viewed with great importance. I actually have a strong interest in this issue as well, and am engaged in discussions with researchers across the world about it.
Knot theory is used to analyze the structure of the DNA double helix. There are knots found in objects like neckties which are deeply rooted in our everyday lives, and they are also used in games intended for infants. What about in the study of mathematics? Knot theory is a field that Waseda University is known to excel in, and the relationships between it and the fields of mathematical theory and mathematical fluid dynamics, which have traditionally been among Waseda’s strengths as well, are receiving great attention. In such ways, knot theory is linked to a number of different fields, with its research continuing to move forward and bring about new perspectives.
Aside from determining its value to other fields, such as how it could be useful to accomplish a certain goal, knot theory has other important merits. When doing research into “the gap between intuition and logic in human spatial awareness”, which was part of the problem I would like to personally pursue as described in the beginning of this article, it cannot be disputed that “knot mathematics” is a study which in itself has great significance. If asked the question of how mathematics can be useful, knot theory can be undeniably considered as both “mathematics with value to other fields” and “mathematics with its own inherent value”.
Understanding Through Logic
From this point on, I would like to strive even more to contribute to our world, and within it to the solution of spatial structure, through the study of knots. Furthermore, I would like to develop and formulate research topics of great interest – that is, the “problems” that we refer to in mathematics – and to cultivate new, undiscovered ground by doing so.
Additionally, I would like to find and create examples where things that seem visible intuitively cannot be deeply understood (that is, they cannot be truly seen) without using logical thinking, to communicate the importance of a mathematics-oriented viewpoint and the significance of mathematics itself. In order to come even a few steps closer to this goal, I would like to arrange situations where free and open discussions can be held regardless of the boundaries of age or standing, without losing our true intentions and sense of humility toward our research.
Interview and composition: Seiko Aoyama / Ryo Oneda
Figure: Noboru Ito / Yusuke Takimura
With cooperation from: Waseda University Graduate School of Political Science J-School










