
- 本間裕大(Yudai Honma)助教(2011年3月当時)
社会の流動は「血流」に同じ
我々が生活を営む社会では、毎日多種多様な「流動」が発生しています。例えば、通勤、旅行といった人の流れや物流、金融システムがあげられます。このような流動がいったん滞ると、社会生活は立ち行かなくなってしまいます。まさに、流動は血流のような存在といってよいでしょう。私は、このような情報社会システムにおける様々な流動を、数学を用いて適切に推定し、また、制御する手法について研究しています。
私がこの研究分野を志したきっかけは、大学で都市を数学的に解析する「都市解析」なる分野と出会ったことです。子供の頃から数学が好きで、かつ、街づくりに興味を持っていたこともあり、とても魅力的な研究分野に感じました。興味が尽きることのない学問とのめぐりあわせに心から感謝しつつ、日々、研究に邁進しています。
数学による流動予測とは
社会における流動を調べる方法の一つに、アンケートを使った大規模調査があります。このような調査で得られるデータは、都市を整備するために必須の、様々な情報を含んでいます。しかし、多数にわたる流動を網羅的に調べるのは簡単なことではなく、調査の終了までに年単位での時間を要してしまいます。数学的に流動を「推定」する意義は、この点にあります。例えば、訪問者数といった断片的なデータから、調査できない年次や他の流動について推定できれば、大幅な費用削減になるのみならず、複数の流動を同時並行で調べることが可能となります。
一例として、人の動きに着目し、ある出発点から目的地までという、2点間で定義される流動を推定することを考えてみましょう。このようなモデル化は、一般に「空間相互作用モデル」と呼ばれており、次の2つのモデル体系で定式化されていることがほとんどです。一つは「システム全体の大域的最適化」という考え方で、これは都市全体を一つのシステムと見なし、全員が協力しあうことによって流動はなんらかの望ましい状態へと落ち着いているに違いない、と仮定するモデルです。統計力学の手法を使い、エントロピー(ちらばり度)が最大となるよう流動を推定するエントロピー・モデルなどがよく知られています。一方、「システム構成要素の利己的最適化」という考え方もあります。この場合、各個人は自分の満足度を最大化するように行動するものと仮定し、流動を推定します。通常ならば、人々は自分の意思に基づいて自由に行動するはずなので、後者のモデル化の方が、より現実社会の仕組みを考慮していると言えます。
実は面白いことに、これら二つのモデルが、ある条件下では互いに等価な数式になることが知られています。このことは、個人の選択行動をうまく誘導することによって、社会にとってより好ましい状態へと導きうる可能性があることを、示唆しています。例えば、近年ではETCの導入により、時間や区間に応じて柔軟に料金割引が設定されていることがありますが、これは「混雑の緩和」という社会全体の最適化を目指したものです。その際の具体的な割引方法の決定などに、上で述べた2モデルの等価性が、適切に用いられています。
連続的な移動をつかまえた
しかし、上述の研究成果について学び、応用分析を行っていくにつれ、既存の数式モデルでは、十分に実社会の流動を表現しきれないことに気付き始めました。最も大きな要因は、これまでのモデルが、出発地から目的地までという、2点間のみでの流動を解析対象としている点にあります。私たちが行う日々の移動行動を想像すると、理解しやすいのですが、実際には、自宅(出発地)から大学(目的地)までで移動が完結することは稀で、その後、飲食店に寄ったり百貨店に寄ったりと、複数の目的地を連続的に訪問しながら移動することのほうが多いのではないでしょうか。私は、このように複数の流動が連続的に発生する現象を「連鎖的流動」と呼ぶことにし、その推定と制御をするための数理モデルについて、研究を進めています。
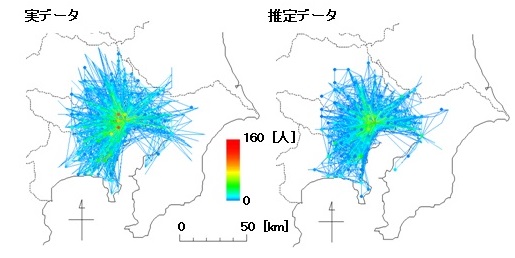
図1 東京圏における周回行動の再現性(提供/本間裕大助教)
話を簡略化するために、複数の目的地をたずねて出発点に戻ってくる周回行動に限定し、その研究成果の一例を紹介します。まず、既存の定式化を拡張し、目的地が複数あるような周回行動を記述するためのモデルを提案しました。すなわち、従来のような目的地が1つだけの移動行動のみならず、目的地が2つ、あるいは3つ、4つといった移動行動も同時に考慮し、より現実的な流動を記述しうるようにしたわけです。さらに、このモデルの再現性を検証するために、2002 年にアンケート調査された東京圏に在住する1万人分の周回行動データと比較してみたものが図1です。左が実際の流動データ、右が提案モデルによって推定された流動データです。いわゆるベッドタウンから都心へ通勤し、その内部で周遊している様子が、よく再現できていることが見て取れます。さて、連鎖的流動を取り扱う際、ポイントとなるのが、いかにモデルの計算量を抑えるか、という点です。連鎖的流動では、複数目的地を自由に組み合わせられるため、より多彩な流動パターンを考慮できるのですが、これは同時にモデル内で取り扱う流動パターンの数が爆発的に増加してしまうことを意味します。したがって、従来と同じ手法で連鎖的流動を取り扱っていたのでは、計算が著しく煩雑になってしまいます。この問題点を解決すべく、人々の移動行動をおみくじ(確率)によって決定させるという、便宜的な「確率的移動モデル」を考えました。おみくじをすべての目的地に設定し、ある目的地に着くと次の目的地が確率的に定まるようにしたわけです。ここでうまく条件を選ぶと、「大域的最適化モデル」、「利己的最適化モデル」に加えて、新たに提案した「確率的移動モデル」を含めた三者が、互いに等価となることがわかりました。この「連鎖的流動モデルの等価性」に着目することによって、システム内の連鎖的流動を推定するまでの計算量を劇的に減少させることに成功しました。実際にはあり得ない「おみくじによるランダムな移動行動」を、思考実験として導入したからこそのブレイクスルーといってよいでしょう。
モデルの応用と展望
「連鎖的流動モデルの等価性」に着目することによって、現在は、情報ネットワークのルーティング制御への応用も試みています。「大域的最適化モデル」によって、情報システムの最適性を保証しつつ、それを「確率的移動モデル」による各制御機器レベルの自律的な分散制御へと、変換させることに成功しています。さらなる性能向上を模索すべく、シミュレーション・実機、両面から検証を進めているところです(図2)。
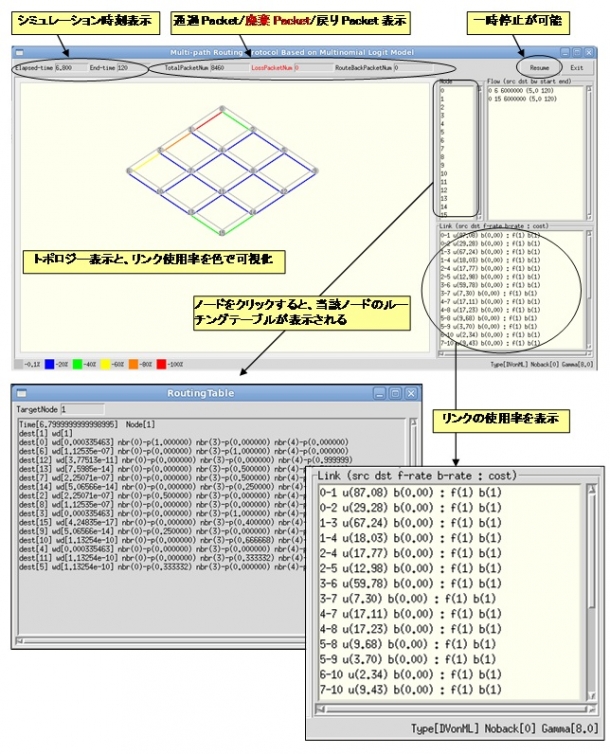
図2 連鎖的流動モデルによる情報ネットワーク制御のシミュレーション(提供/本間裕大助教)
今後は、各種の産業連関や移動手段に着目した連鎖的流動を捕え、日本中の都市活動を対象としたダイナミクスについても調べたいと思っています。都市活動分布と連鎖的流動の相互連関構造を明らかにすることで、複数の都市が互いに影響を与えながら発展するヒントが得られそうです。将来的に、日本全体を発展させる一助になればと考えています。
取材・構成:青山聖子、名古屋大学 大住克史
協力:早稲田大学大学院政治学研究科J-School










