When using mathematical models in the sciences, problems often boil down to solving equations. These are often equations governing how a system evolves with time, either in a continuous way (differential equations) or discrete way (difference equations).
If such equations have a property called nonlinearity, then in general they cannot be solved exactly and the systems they describe are chaotic. However, among nonlinear equations there are special examples in which, rather than chaos, the system exhibits regular behaviour and an abundance of symmetry. The field of study of these exceptional examples is known as (nonlinear) integrable systems. My research involves studying integrable systems using methods and ideas from geometry.
Integrable systems and mathematical phenomenology
The history of integrable systems as an area of mathematics goes back to observations made by Scottish engineer John Scott Russell in 1834 while doing experiments related to the design of hulls of canal boats. These experiments involved pulling a boat along a narrow canal by a pair of horses. At one point the horses and boat suddenly stop, and a wave forms and travels forward from the bow of the boat. Rather than dissipating as one might expect, the lump of water travels along the canal at a constant speed without changing shape. Russell chased the lump of water along the canal on horseback, calling the “singular and beautiful phenomenon” he observed the “Wave of Translation”.
Russell’s observations led to a search for an explanation – a kind of mathematical phenomenology. Rayleigh and Boussinesq made theoretical models for the kind of situation in which the wave of translation was observed, and Korteweg and de Vries in 1895 proposed the nonlinear partial differential equation 
for the height u(x,t) of water at position x and time t, now known as the Korteweg-de Vries (KdV) equation. In the 1960’s in the US, Zabusky and Kruskal performed numerical simulations of solutions of the KdV equation and demonstrated travelling localised waves, which they called solitons.
Figure 1: Snapshots of a soliton solution of the KdV equation, evolving in time from left to right
In 1967, Gardner, Greene, Kruskal and Miura showed that the KdV equation could be solved exactly under certain assumptions, using a method called the inverse scattering transform. The KdV equation and other nonlinear partial differential equations solved by inverse scattering are examples of nonlinear integrable systems. Despite their exceptional nature, integrable systems appear surprisingly often in models in diverse areas of natural sciences, including nonlinear waves, optics, statistical mechanics and quantum gravity.
I find integrable systems to be an exciting area to work in, for the following reasons.
- Mathematical richness.
Integrable systems possess a lot of mathematical structure, which makes them amenable to study using varied mathematical tools, particularly from algebra and geometry. - Mathematical phenomenology.
If we find integrability or exceptional behaviour associated with it, we want to explain why. Integrability can often be understood in terms of geometry, and this leads to deep questions and the development of new mathematics.
My research involves equations whose special properties can be understood in terms of associated geometric objects, but the history of these goes back before solitons to the search for new mathematical functions.
Painlevé equations and geometry
Many functions used in mathematics, physics and engineering satisfy linear differential equations. Around the turn of the 20th century, Paul Painlevé (who would later go on to become Prime Minister of France) and his student Bertrand Gambier embarked on a program to find differential equations which, despite being nonlinear, could be used to define functions. Within a large class of equations they found 50 classes, with six of these not solvable in terms of known functions. These six, now known as the Painlevé equations, define new transcendental functions and are related to integrable partial differential equations. They can be regarded as integrable systems in two dimensions and have many properties associated with integrability, for example an abundance of symmetry.
In the late 1970’s, Kazuo Okamoto constructed a geometric object associated with each Painlevé equation called the space of initial values, which provides a space on which singularities of the equation are resolved. This is constructed using a technique from algebraic geometry called a blowup, and many properties of the equation can be understood in terms of the geometry of the space of initial values. After Okamoto’s work, Kyoichi Takano and collaborators showed that Okamoto’s space in a sense characterises the corresponding equation uniquely. This is interpreted to mean that the space carries all memory of the equation and its properties – ‘geometry tells us everything’.
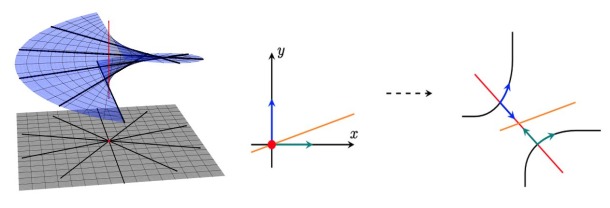
Figure 2: Schematic representation of a blowup – a surgery which replaces a point on a surface with a line, in a way that separates lines passing through the point according to their slopes.
There are also discrete Painlevé equations, which provide two-dimensional models like their differential counterparts but with evolution in discrete steps. Discrete Painlevé equations are in many ways more fundamental and mathematically richer, and a unified geometric framework for both differential and discrete Painlevé equations was developed by Hidetaka Sakai in terms of associated geometric objects generalising those constructed by Okamoto. My research involves both using this geometric framework to solve problems related to differential and discrete Painlevé equations, as well as extending elements of it to wider classes of equations.
Past research
I first encountered integrable systems and Painlevé equations while an undergraduate student at the University of Sydney in Australia. My majors were in Mathematics and Japanese Studies, and when, in my third year, I was looking for opportunities to try out research projects in mathematics, one of my professors suggested I approach Professor Nalini Joshi AO because she had ongoing collaborations with Japanese mathematicians. I went on to complete Honours in Applied Mathematics at the University of Sydney, with my research project supervised by Professor Joshi with assistance from Dr Nobutaka Nakazono and Dr Yang Shi. I then went on to PhD studies in Mathematics at University College London supervised by Professor Rod Halburd. After graduating in 2020 I held a London Mathematical Society Early Career Fellowship then came to Japan in November 2021, to take up a Japan Society for the Promotion of Science (JSPS) Fellowship for two years at the University of Tokyo hosted by Professor Ralph Willox. I was then at Warsaw University before joining WIAS in April 2024.
My work so far has involved both applying and extending the geometric theory of Painlevé equations and their discrete analogues.
One example of an application was to certain solutions of the Sasa-Satsuma equation, which is used to model waves in optics and is integrable in a similar sense to the KdV equation discussed above. Recently Professor Jianke Yang and Dr Bo Yang constructed a family of solutions of this equation, some of which constitute ‘partial-rogue waves’, which they described as “waves that come from nowhere but leave with a trace”. Which of the solutions constitute partial-rogue waves is predicated on something that was previously unknown about certain solutions of the fourth Painlevé equation. With Dr Pieter Roffelsen we used elements of the geometric framework to settle this and describe exactly which solutions constitute partial-rogue waves.
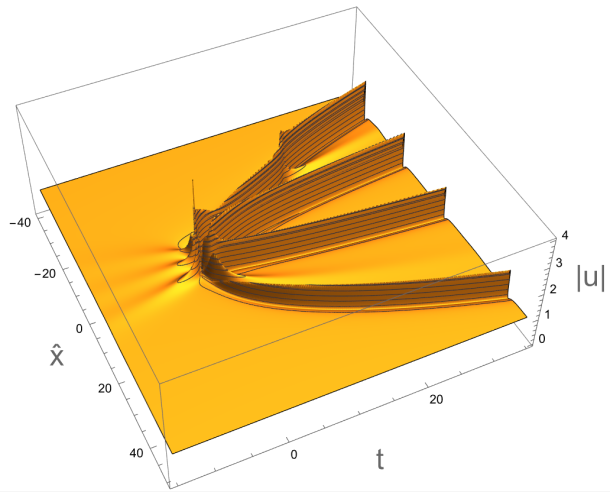
Figure 3: One of the solutions of the Sasa-Satsuma equation that constitutes a partial-rogue wave.
Another example, which involves discrete Painlevé equations, is that with Professors Anton Dzhamay and Galina Filipuk we developed a geometric procedure for solving the Painlevé equivalence problem. This asks, if a system of differential or difference equations are either known or suspected to be equivalent to a differential or discrete Painlevé equation how to find an explicit transformation realising this. The procedure involves finding the transformation on the level of geometry and has been applied to instances of differential and discrete Painlevé equations appearing in the theory of orthogonal polynomials and related probabilistic models.
Current research and future aspirations
I am currently investigating geometric descriptions of analogues of Painlevé equations beyond the known two-dimensional case: discrete equations in higher dimensions and delay-differential equations, which are used to model systems whose evolutions depend on their past states, for example in economics and climate science. The geometry of several examples of discrete Painlevé equations in higher dimensions has been established, but there is not yet a general theory. Similarly, some geometric features of delay-differential Painlevé equations have been discovered, but the picture is incomplete. The ultimate aspiration of this research direction would be a general geometric framework for higher-dimensional discrete Painlevé equations and delay-differential Painlevé equations.
In both the higher-dimensional discrete and the delay-differential cases, there are various parallels with the development of the theory of discrete Painlevé equations prior to the Sakai framework. These suggest an underlying geometric picture exists, and the quest to uncover it is again a kind of mathematical phenomenology.
