
量子技術研究に携わることになったきっかけ
私たちの周りの物質は原子や分子からできています。それぞれの原子や分子をレゴブロックとして考えてみましょう。これらのレゴブロックを組み合わせることで、生き物から建物までさまざまなものの形を作り出すことができます。私は、こうした個々の要素が集まることで初めて現れる現象に興味をもっており、統計力学と量子計算科学の研究を行っています。統計力学は、多くのレゴブロックが集まることで現れる物質の性質を明らかにする学問です。氷、水、水蒸気といった異なる性質が同じ水分子から現れることは非常に面白いことです。

図 1個々の要素が集まることで現れる現象 https://www.pony-t.co.jp/categorize/toys/page/9/
一方、量子計算科学は、多くのレゴブロックを適切に組み合わせることで問題を解く方法を明らかにする学問です。この二つの分野は一見全く異なるように見えますが、個々の要素が多数集まったシステムの性質を理解するという共通の目標を持ちます。この観点から、私は統計力学と量子計算科学との融合領域を開拓したいと考えています。とくに、量子ビットと呼ばれる少し風変わりな性質をもつレゴブロックで構成された計算機である量子計算機を効率的に利用する方法や、量子計算機を用いて統計力学の問題を探究することに興味があります。
私は、統計力学を専門とする宮下精二教授(2011.4-2016.3)のもとで学位を取得しました。その後、中村壮伸助教(2016.4-2016.12)のもとで材料と数学の融合分野の研究をしました。当時、中村先生が「材料の研究をするとどんな背景をもつ人とも話ができる」という主旨の話をされていたことをよく覚えています。私もいつか異なる背景をもった方と自身の専門性を活かした研究ができたらと感じていたところ、ちょうど田中宗准教授に声を掛けていただき、情報工学を専門とする戸川望教授と量子計算科学の研究をする機会を得ました(2019.4-2024.3)。
量子技術は、現代社会のさまざまな面を劇的に変える可能性をもち、産業界を巻き込んで現在世界中で活発に研究が行われています。たとえば、高感度で高空間分解能の量子センサ、量子状態を利用した暗号技術、高性能な量子デバイス、複雑な問題を解く量子計算機の実現に向けた研究が行われています。量子計算機の活用が期待されている問題として組合せ最適化問題があります。組合せ最適化は、多数の選択肢の中から、制約(ルール)を守りつつ、目的関数を最小化もしくは最大化する選択肢(最適解)を見つける問題です。これらの問題は、物流、通信、創薬、金融といったさまざまな領域に現れます。
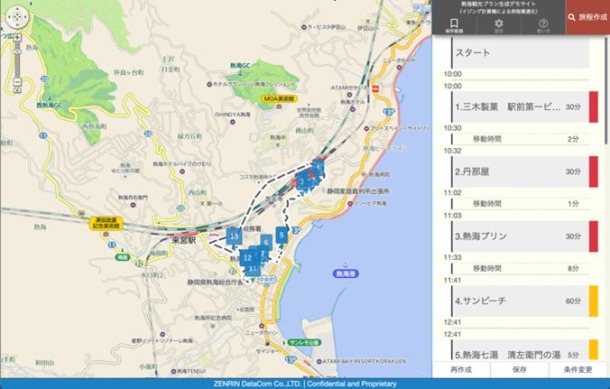
図 2観光プラン生成アプリケーション
http://at-lab.its-mo.com/trip/atami/
図2は、株式会社ゼンリンデータコムと私たちのグループが共同で作成した熱海市の観光プランを生成するアプリケーションのデモです。擬似量子計算機(量子計算機を模した計算機、将来的に量子計算機に置き換わる可能性をもつ。)を用いて、旅行テーマ、施設、観光スポット、グルメ、交通手段などのさまざまな好み(制約)に基づいて満足度を最大化する旅程を計算します。これは、私たちが日常的に量子技術をどのように活用するかを示しており、将来実現する量子社会を想像させてくれます。
量子技術の実用化に向けた研究
量子計算機で行う計算は、従来の計算機やスーパーコンピュータでも非常に長い時間がかかると考えられており、このことから量子計算機を用いてこれまで困難であった問題を解決できると期待されています。たとえば、素因数分解(2024=2×2×2×11×23)を高速に行う量子アルゴリズムが提案されています。しかし、このアルゴリズムは量子計算機で複雑な計算を誤りなく行う必要があり、現在開発されているエラーのある量子計算機では、実用的な応用に限界があります。
現在の量子計算機の限界を克服すべく、多くの研究者が量子計算機を用いて実用的な問題を解くために必要なハードウェア開発に取り組んでいます。現在、数十から約千までの量子ビットをもつさまざまなタイプの量子計算機で計算が可能です。たとえば、早稲田大学と提携しているOxford Quantum Circuits社が開発した量子計算機Toshikoは32個の量子ビットをもちます。さらに、内閣府が提唱する量子未来社会ビジョンでは、2030年までに1,000量子ビットをもつ量子計算機がより容易に利用可能になると予測されています。このように、量子計算機のハードウェアの進歩は目覚ましく、そうした量子計算機を利用するための環境が整ってきたことは、とてもワクワクすることです。
量子計算機を用いた実用的な応用の実現には、ハードウェアの進歩だけでなく、それを利用するためのソフトウェアの開発も重要です。たとえば、組合せ最適化問題を量子計算機で解く場合、イジング模型の基底状態を探索するソフトウェアを用います。イジング模型は複数の+1もしくは-1をとる二値変数(これをスピン変数と呼ぶ)の関数であり、スピン変数の組み合わせによって値(これをエネルギーと呼ぶ)が変化します。図3(左)は、2個のスピン変数からなるイジング模型のエネルギー地形を示しています(上矢印と下矢印はそれぞれスピン変数が+1、-1を表す)。組合せ最適化問題の最適解を、イジング模型の基底状態(エネルギーを最小化するスピン変数の組み合わせ)として表すことで、このソフトウェアを利用することができます。
しかし、実用的な組合せ最適化問題を量子計算機で解くことはまだ困難です。その一つの原因は、イジング模型のエネルギー地形に多数の局所最適解が存在することです。局所最適解とは、周囲の解と比較して、局所的にエネルギーが小さい解(図3左で一つ目のスピンが+1、二つ目のスピンが-1の解)を指します。局所最適解からより低いエネルギーの解(図3左で一つ目のスピンが-1、二つ目のスピンが+1の解)に到達するためには、途中で高いエネルギーの解を経由する必要があります。しかし、一般に低いエネルギーの解から高いエネルギーの解への遷移は困難であり、このことが組合せ最適化問題を解く手法の精度を低下させます。私は、量子ソフトウェアの性能を改善し、組合せ最適化問題を解きやすくするための手法開発に取り組んでいます。たとえば、イジング模型が与えるエネルギー地形を変形し(図3左から図3右に変形し)、局所最適解から効率よく脱出する機構を与える方法について研究しています。
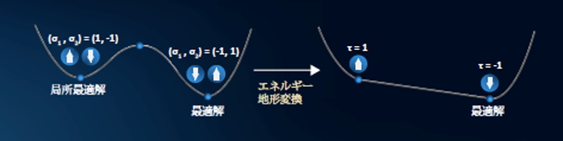
図 3エネルギー地形を変換して組合せ最適化問題を解きやすくする技術
(早稲田大学プレスリリース資料より https://www.waseda.jp/top/en/news/75957)
今後の抱負
量子技術は、さまざまな分野においてこれまで不可能であると考えられてきた技術を実現する可能性を秘めています。量子技術の分野の大きな特徴は、多様なバックグラウンドをもつ研究者、専門家、エンジニアが知識を共有しながら研究開発に取り組んでいることです。私はもともと統計力学の理論研究を行っていましたが、2019年に早稲田大学に移ってからは、情報工学の領域で統計力学の知識を活かした研究活動を行ってきました。異なる考え方に刺激を受けることで、研究に対して新しい視点から取り組むことができたことは非常に新鮮な経験となりました。また、高等研究所には多様なバックグラウンドをもつ研究者が集まっています。これらの機会を活かし、さまざまな領域の研究から刺激を受けながら、統計力学と量子計算科学の融合領域を開拓していきたいと考えています。










