
- 伊藤昇(Noboru Ito) 助教(2014年1月当時)
結び目
目の前で裁縫か何かをしているときに、図1の左側のように複雑になってしまった紐があったとします。これは、右側のようにほどけるでしょうか。見た目ですぐに判別するのはなかなか難しいと思います。私を含め、思春期に皆一度は「自分とは何なのか」と悩むように、そこに存在し、実際に眺めることができ、しかも手に取ることができるにもかかわらず、それに対する理解が容易でないという場面があります。
空間認識の代表的ツールである「結び目」を通して、上述のような直感と理解の狭間を飛び越える「難しさ」を解き明かしたい、これが私の個人的な問題意識です。

図1:複雑になって閉じてしまった紐とほどけた紐
結び目の研究方法
では複雑な結び目をどうやって判別するのでしょうか? 方策を整理してみると次の2つになります。
Ⅰ.2つの結び目が異なることを証明すること
Ⅱ.2つの結び目が同じであることを証明すること
まずⅠの考え方を説明します。例えば、ゴムボールと一人用の浮き輪が目の前にあるとします。私たちは何を用いてこれらを「違う」と認識しているのでしょう? 例えば穴の数を使ってゴムボールと浮き輪を見比べると、一方は穴の数が0個、他方は1個です。「図形と数を対応させること」、「0と1は異なる数だということ」、この2つの「数学」を使って図形を判別するのです。結び目の判別も類似の仕組みを使います。図形と数を対応させる仕組みを現代数学では「不変量」と呼びます。後で例をあげますが、私は昨年も今年も新たに図形の不変量を創り出して研究を進めてきています。
次にⅡで使われる方法について説明します。一方の結び目から他方の結び目に移る変形の過程が3種類の局所的な紐の動かし方(図2・上段)によるもので与えられたなら、2つの結び目は同じです。すなわち、一方から他方へ結び目の変形過程を分解して書き表し、3種類の変形からなる列を見つけさえすれば、2つの結び目が同じであるということを厳密に証明することができるのです。例えば図1の場合も、左の結び目に3種類の変形を次々に上手に施していくと、右のほどけた図になっていきます。

図2:結び目の3種類の局所変形(上段)、対応する影に関する局所変形(中段)、2種類のRⅢ(下段、点線はつながり具合を表している)
結び目の影だけを見てみましょう。すべての影は図2の中段にある3種類の変形により、◯(丸)になります。では、影の動きを制限したときも、私たちは結び目の影の動きをとらえられるでしょうか?3通り考えてみましょう。
・Case 1:RⅠのみを禁止する。
・Case 2:RⅡのみを禁止する。
・Case 3:RⅢのみを禁止する。
Case 1は1937年に既に解決されています。ところがCase 2は現代の最先端の研究でもほとんどわかっていません。そこで私はRⅢを2種類(wRⅢ、sRⅢ)に分け、谷山公規先生(早大教育・教授)や瀧村祐介氏(早大教育・修士2年)と協力し、それぞれに関して問題の一部を突破しました。この中で、RⅠとsRⅢを用いた変形(strong(1, 3)と命名)において3で割った余りが不変量になるX(P)という量を私は発見しました(図3)。なお、Case 3については瀧村氏と私の共著論文(2014年出版)が完全な解決を与えています。
私は日独共同大学院プログラム(日本側コーディネーター:柴田良弘先生[早大基幹理工・教授])に参加させていただいたことがきっかけで、2009年から海外で講演させていただくようになりました。その中で2010年に、幸いにも著名な数学者Oleg Viro先生(Stony Brook University・教授)と面識を得ることができ、ご助言をいただくようになりました。それから3年余、最初にお会いした折にいただいた「Viro先生からの宿題」に対しての最初の足がかりがようやく見えてきました。
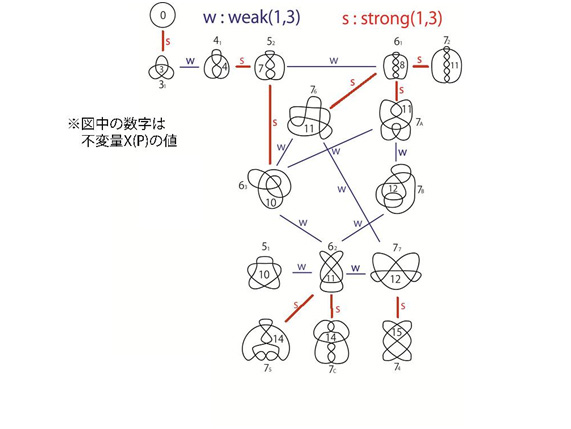
図 3:赤線で示された変形では、図中のX(P)(mod 3)が不変であることがわかる
数学者の頭の中
私の頭の中には常に三つ四つの問題が入っています。それは1年程で解けそうな未解決問題から、10年単位の大未解決問題のようなものまでいくつかのレベルがあります。もちろん、先ほどのViro先生の宿題も入っています。
その一方で私は毎日必ず数学しか考えない時間を数時間設けるようにしています。これは早稲田大学の江田勝哉先生(早大基幹理工・教授)が「毎日3時間以上」として数学系の学部生に守るようにおっしゃっていることです。以来3時間は最低ラインと認識し、学部生時代からずっと守り続けています。江田先生曰く「毎日と言えば毎日なのです」。それは盆も正月も土日も関係なく、1日も欠かさないという意味です。これを続けていると、さまざまなことができるようになります。最初は一見とりつきにくい数学概念も次第に頭になじむようになってきます。また、何段階もの証明を散歩しながら考えられるようにもなります。そして、ある日のある時「あぁ、解けたな」という瞬間が訪れます。問題といつもいっしょにいるように努めれば、自然な形で答えをもってやってくる問題もあるのです。
結び目理論はどう役に立つか
結び目理論はガウスの時代から電磁気学との関係がありました。それ以降、結び目理論は物理学と相互に影響し合っています。特に、80年代からは物理的背景をもつ「量子不変量」に関する理論が数学・物理学で大発展しています。量子場の理論と量子不変量を念頭においたときは、粒子が飛び回った軌跡(=粒子の一生)を結び目とみたりします。さらに踏み込んで、ここ最近では、弦理論における結び目理論の役割というものが重要視されています。この問題には私も深く興味をもち、世界中の研究者と議論し、取り組んでいます。
DNAの二重らせんの構造解析にも結び目理論は使われています。また、ネクタイのように生活に根ざした結び目もありますし、幼児向けのゲームにも使われています。数学の中では、どうでしょう。例えば、結び目理論は早稲田大学が強いとされる分野であり、同じ早稲田大学で伝統的に強い数論や流体数学との関係が注目されています。このように結び目理論は、実にさまざまな分野と関係し、研究を推進し、新たな視点をもたらしています。
結び目理論には、「◯◯の役に立つ」という他分野へ価値を求める以外にも価値があります。冒頭で述べたように私個人の問題意識の一つである「人間の空間認識における直感と論理のズレ」も研究している点において、「結び目の数学」は、それ自体に存在意義のある研究に他ならないのです。「数学がどう役に立つか」という問いかけに対して、「他分野に価値がある数学」も「一人称による数学の価値」も確かにここにあるのです。
論理を通して理解する
今後、結び目を通して、この世界、中でも空間構造の解明に貢献できるよういっそう努めていきたいと思います。さらに、非常に興味深い研究対象―それは数学でいう「問題」そのものなのですが―を発掘・生成し、新しいフィールドを開拓したいと考えています。
そして、直感的に見えているものでも論理を通さないと深く理解できない(ほんとうに見えたことにならない)という場合の例を見いだしたりつくりだしたりして、数理的視点の大切さや数学の存在意義を発信していけたらと考えています。これらの目標に一歩でも二歩でも近づけるように、研究対象に対して素心や謙虚さを失わず、年齢や立場の垣根を超えて自由闊達に議論できる場を生み出していきたいと思います。
取材・構成:青山聖子/大根田諒
図版作成:伊藤昇/瀧村祐介
協力:早稲田大学大学院政治学研究科J-School










