
- 門内隆明(Takaaki Monnai)助教(2013年11月当時)
熱平衡と非平衡
私は2003年以来、一貫して非平衡統計力学の構築に取り組んでいます。これは時間不可逆性の起源にも深く関係する壮大なテーマなので、いくつかのプロジェクトを並行して進めており、ここでは量子力学が内包する確率(スペクトル揺らぎ)に基づく理論について紹介します。
非平衡系という言葉は聞き慣れないかもしれませんが、「動き(ダイナミクス)」のある状況のことです。例えば、コーヒーにミルクを入れ、充分時間が経過すると均一に混ざったミルクコーヒーになります。そして、いったん均一になると、マクロにはこれ以上変化しません。このように物質系が行きつく「均衡(バランス)」のとれた状態のことを「熱平衡」と言います。一方、コーヒーとミルクが混ざる途中の過程のようなダイナミックな状況を「非平衡」と言い、輸送現象をはじめ多くの興味深い現象は非平衡系で起こります。
極めて非自明なことですが平衡状態においては、莫大な数の要素(原子や分子)からなる物質について様々な物理量を定量的に計算できます。この意味で、平衡統計力学の基本的部分については理解が進んでいます。
一方、非平衡系では多彩なダイナミクスがある分、考慮する要素が増えるので、理論構造ははるかに複雑になります。
それでもなお、ナノスケール(ナノメートルは1mの10億分の1)における輸送現象や孤立量子系における熱平衡化等については、統計力学の自然な拡張が可能で、まさに現代物理学における最も挑戦的な課題の一つであると言えます。
統計力学の抱える問題点を量子力学で解決する
従来の統計力学では、原子や分子の基本法則と日常的な経験則を、確率概念を用いて整合させていました。
ここでの考え方は、例えて言えば、アンケート調査のようなものです。これは個別の被験者がどういう状態にあるかまでは問わず、特定の性質に該当する人数だけに情報量を落とすことで、分布の特徴を把握します。その際、無作為に被験者を選ぶということがとても大切です。
しかし、熱平衡にある物質系において、どんな状態をどういう基準で選べば無作為な抽出になるかは難問です。そこで、統計力学では無作為なサンプリングをしていると仮定する「等重率の原理」を用いて、統計平均を測定値と結び付ける「エルゴード仮説」によって計算を進めます。そうして計算した統計力学の理論値は実験とよく合うのです。しかし、これらの統計仮説は満たされない場合が多いということがこの手法の問題点です。
一方で、量子力学という確率の概念を内包している力学が知られています。
そこで、外から勝手に「等重率の原理」や「エルゴード仮説」のような統計的仮定を入れるのではなくて、量子力学が内包する確率(スペクトル揺らぎ)を中心にして統計力学を書きなおそう、という試みが国内外で進められてきました。
ここでは詳しい説明は述べませんが、この方法だと「エルゴード仮説」は(それ自身興味深く有益なことも多いのですが)仮定する必要がなく、「等重率の原理」も、ごく自然に理解できます。
非平衡系への応用
多くの研究者は「量子力学を用いた新しい統計力学は平衡状態にのみ適用可能である」と考えていました。これは、非平衡物理量による系全体にわたる任意の相関の検出という問題と関係しており、一見尤もらしいです。しかし、私は「平衡状態から出発する非平衡過程」には適用できると考えました。
これを検証するため、鉄などの強磁性体をモデル化した一次元斜め磁場イジングモデルという系(図1)に対して、外から振動磁場(図1 B青矢印)を加えるという非平衡過程において、エントロピー生成という物理量のスペクトル揺らぎに関する分布関数を計算しました。
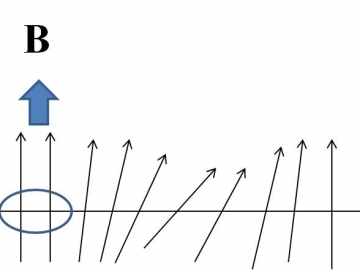
図1:強磁性体のイジングモデルの概念図。矢印の向きが電子スピンの方向を表す。楕円中のスピンにBの青矢印で示した振動磁場を加えると、エントロピー生成が起こる。
左端2つの電子スピンに対して局所的に振動磁場をかけてエネルギーを注入すると右の電子スピンに伝播し、エントロピー生成が起こります。この一連の過程を1回の実験とみなすと、エントロピー生成の値は「不確定性原理」と「熱揺らぎ」という2つの確率的な要素によって再現性なく毎回異なる値をとります。図2は初期状態が統計力学を用いた熱平衡アンサンブルの場合(赤線)と量子力学における典型的純粋状態の場合(青点列)のエントロピー生成の生起確率を比較しています。両者は、理論で計算される誤差の範囲で一致しています。
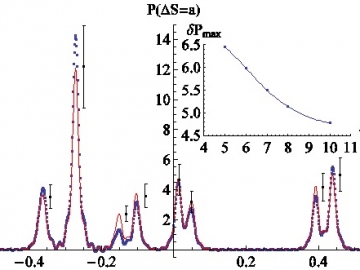
図2:斜め磁場イジング模型に印加した振動磁場によるエントロピー生成ΔSの分布関数。 横軸はエントロピー生成量を、縦軸はその生起確率を表す。1つの純粋状態を用いて計算した青の点列と初期熱平衡アンサンブルを用いた赤線が、理論的に計算した標準偏差の範囲で一致することを確認できた。 ピークが連続して現れていないのは、本図で用いた低温パラメータの場合、電子状態のエネルギー準位間で可能な遷移が限定されるためと考えられる。 右上のグラフはシステムサイズNを増やすと、赤線と青点列のずれ(δPmax)は小さくなることを示す。
量子力学における純粋状態を用いた計算の大きな利点は、平均から大きく外れている「大偏差」を正確に解析できることです。分布関数の裾にあたる大偏差領域は、上の例で言えば、「非常に数は少ないけれど、極端に大きな(或いは小さな)エントロピー生成が起こること」に相当します。このようなデータは数が少ないため、実験的にも扱うのが困難で、通常大きな誤差を伴います。これに対し、量子力学が内包する確率を用いると、1つの純粋状態だけを用いることで生起確率の低い大偏差領域まで含めて定量的に正しく解析できるのです。
これからの研究
ここで紹介したように、従来別々に考えられてきた統計力学と量子力学を融合させることで、無理なく確率を導入することが可能になり、その結果たった1つのサンプルに基づいてミクロとマクロを直結させる方法がわかってきました。しかし、マクロな系を孤立量子系として理解する必要があり、熱平衡状態への接近というごく身近な現象に限っても、従来の散逸を通じた理解とは大きくかけ離れた考え方が要求されています。そのために私は凝縮系や量子光学、量子情報論をはじめ周辺分野と緊密に連携しながら理解を進めていこうと思います。
取材・構成:大石かおり
協力:早稲田大学大学院政治学研究科J-School










