数学を身に付けて社会に出れば、
“大人のうそ”にだまされない

――数学は学校で学ぶ最も基礎的な科目の１つ。しかし、社会では実際にどのように役立つのかが今一つ分かりにくいような印象があります。

この記事を読んでいる学生さんはおそらく、数学が嫌いなのだと思います（笑）。しかし、数学は本来、人間を幸せにするツールです。ビジネスや日常生活、国を動かす政治判断まで、あらゆるシーンで私たちを助けてくれます。最も顕著な例は、データや数値との向き合い方でしょう。

皆さんは就職活動をする際、必ずと言っていいほど、勤め先の「平均給与」を見るのではないでしょうか。その理由は、高い給料をもらいたいから。しかし、平均給与でその判断をするのは本当に正しいのでしょうか。考えてみます。

A社の平均給与が500万円、B社は800万円だとします。平均給与の観点からすると、B社の方が勝っていることは言うまでもありません。しかしここでは、社員によって給与にばらつきがあるのがポイントです。

両社ともデザイン会社で、それぞれ5人の社員がいるとします。A社は一人一人が同様にクライアントを持っていて、5人全員の年収が500万円だとすると、（500万×5）÷5＝で500万円が平均給与です。一方B社にいるのは1人が世界に名を馳(は)せるデザイナーで、残る4人はアシスタント。デザイナーの給与が3,000万円で、他の4人が250万円だとすると、平均給与は（3,000万＋250万×4）÷5＝800万円になります。つまり、あなたが超一流デザイナーでない限り、平均給与の低いA社に入った方が、多くの収入を得られるのです。

ここで紹介した平均給与は、数学の世界で「平均値」と呼ばれます。皆さんもよく知っているのではないでしょうか。しかし収入や人口、貯蓄額というように、数値の分布にばらつきがある現実世界の統計では、平均値を見るだけでは判断しにくいものが多い。その際には「中央値」という値が重視されます。中央値とは、値を大きさ順に並べたときに真ん中に来る数字です。それぞれの会社の給与の中央値を求めると、A社は500万円である一方、B社は250万円となります。こうした知識があれば、「平均給与が高いB社に入社したのに、なぜかもらえる給与が少ない...」と一人で焦ることもないでしょう。

こうして数学は、皆さんを幸せにするんですね。

――情報やデータにだまされないのが、数学の力ということですね？

実社会では、数字を持ち出して“それっぽく”自分の有利な方向に持っていこうとする人がたくさんいます。平均給与の例でも見たように、数字で人をだますことは、簡単にできてしまうのです。

最近、エビデンスという言葉をよく耳にするようになりました。しかし、本当に適切な方法で作成した「エビデンス」を示している人は、ごく一握りのように感じます。メディアに登場する政治家や評論家、ビジネスの現場でやたらとグラフを持ち出すプランナーなど、たとえだます気がなかったとしても、数学的なステップを踏んでいない人が多い。数学が苦手な人は、「エビデンスがある」というだけでそこに食いついてしまうのです。SNSでうわさやデマが拡散されるのも、多くはそのことが原因でしょう。

そもそも数値や統計は、「相関関係」を示すことはできますが、「因果関係」は示せないことが多いのです。以前、新型コロナウイルス感染症に紅茶が効くという説が話題になりました。その説の基となった研究発表では、理想的な状態で紅茶とウイルスを混合すると、ウイルスの感染力が失われることが示されています。ここに間違いはないでしょう。しかし、実際に人間が紅茶を飲んで、その力が発揮されるかを証明するのは非常に困難です。人間の体内には唾液や胃液が存在するなど、試験管の中とは条件が大きく異なるため、正確な臨床実験が難しいからです。現実に紅茶がウイルスの感染力を99.9％無くすことができても、「それがどのような状態で実験した結果なのか」「その結果が別の状態でも起こりうることなのか」ということはこれからの研究に依ります。数値だけの予想ではなく、実際に起こったことでも、いつでも同じ結果が得られるかは、さらに研究が必要です。当然、数値だけの予想しかないときには、より細心の注意を払わなければなりません。

つまり、「ウイルスと紅茶の間には関係がある」ということは分かりますが、「紅茶を飲むと、ウイルスを消滅させられる」という、人に対する優れた効用については、まだ辿(たど)りついていないということです。研究者の細かい実験によって、どのように紅茶を使うと体内のウイルスに対して効果があるかを研究する必要があります。情報の受け手が、エビデンスの1つの側面しか見ていないと、間違った結論を信じてしまうことがあります。

数学をしっかりと勉強すると、世の中にあふれる情報に対して「どこがおかしいのか」を見抜くことができるようになります。近づいてくるうそつきに言い返し、論破することもできるでしょう。へりくつになりすぎると嫌われるので、注意が必要ですが...（笑）。

皆さんが判断を間違えることなく、正しい道を歩むとき、数学は強い武器になるのです。

私たち人類の生活は
数学抜きでは成り立たない

――データを見る力以外でも、数学は私たちを幸せにするのでしょうか？

私たち人類にとって、数学は生きる上での必需品でもあります。医療や建築で計算を間違えると、人の命に関わりますね。豊かな生活を実現している文明は、実は数学抜きでは成り立たないのです。

人類と数学の歴史は、はるか昔にさかのぼります。古代のバビロニアやエジプト、中国、インドの文明では、2次方程式を使って土地や建物の面積を考えていた痕跡があります。ハンムラビ法典では高い金利が禁止されていますが、利率を計算する高度な能力を持っていたことを意味します。これらは全て紀元前の話ですから驚かされます。

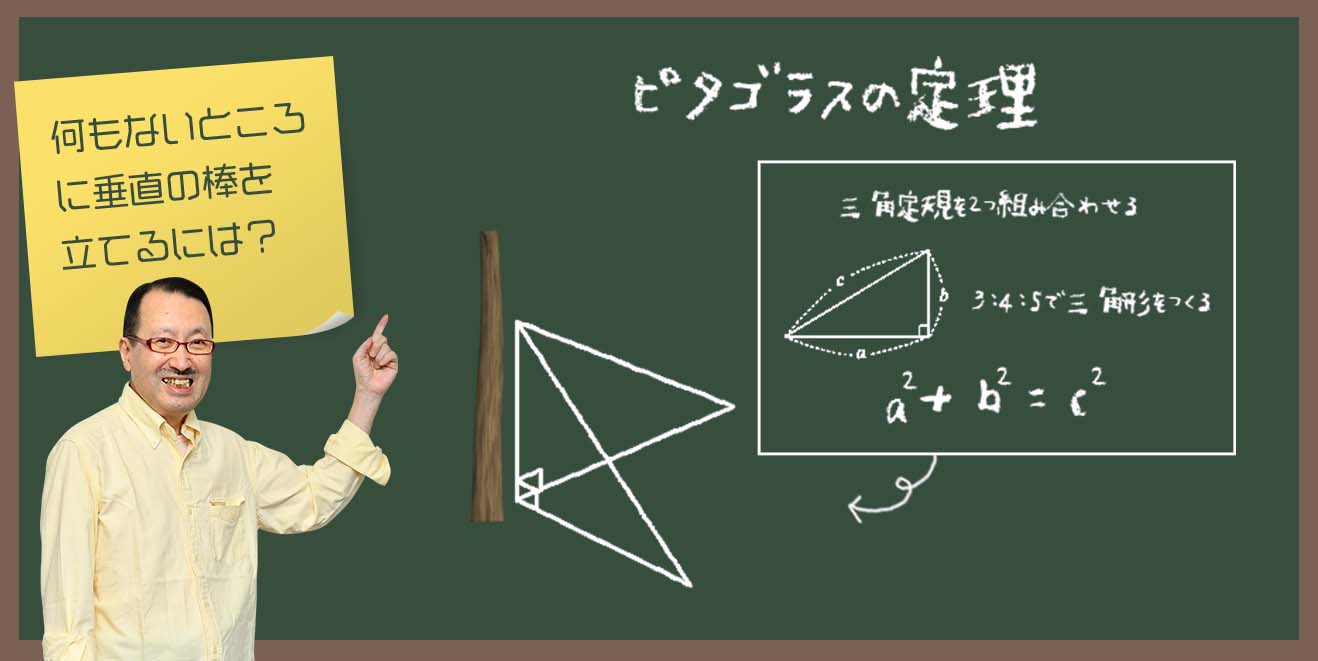
農業に関して詳しく見ていきましょう。雨期の予測が必要となる農業では、1年のサイクルを正確に把握する必要があります。そこでは冬至や夏至など、季節の変わり目を知ることが有効です。しかし古代の人々は、冬至や夏至をどのように調べていたのでしょうか。それを可能にしたのは、地面に垂直に立てた棒でした。太陽の影が最も長くなる日が冬至、短くなる日が夏至だからです。

では、棒をどのように地面に立てればいいのでしょう？ 今日、私たちは2つの直角三角形の定規を使えば、簡単に垂直の棒を立てられます。ただ、古代にそんなものはもちろんないので、定規は自分で作らなければなりません。ここで役立つのが、有名な「ピタゴラスの定理」。直角三角形の3辺の長さに関する、a²+b²=c²という関係です。a²+b²=c²が成立すれば直角三角形となるので、例えばa=4、b=3、c=5を当てはめれば実現できます。あとは三角定規が揺れ動かないように、もう1つ用意すれば完成です。

ピタゴラスの定理という名前は、古代ギリシアのピタゴラスが証明したといわれていることから、ついたものです。しかし、垂直に棒を立てるこの方法は、ピタゴラスが生まれるより前から、世界各地の文明でも使用されていたと考えられます。エジプト文明のピラミッドや、縄文時代の高床式倉庫を傾くことなく建てられたのも、垂直を知る技術があったからでしょう。江戸時代の大工も、3:4:5の直角三角形を使用していました。ピタゴラスの定理を学校で習っていない、世界各地の人たちの知恵が、農業から建築にいたるまで、さまざまな形で文明の基礎を築いてきたのです。ピタゴラスは偉大ですが、ある意味古代人が知っていた定理を数式としてまとめただけのようですね。

よく皆さんが「数学」と聞いて思い浮かべるのは、机の上の数式で表現される、近代的な数学のこと。それ以外にも数学は、私たちの身近なところで生活を支えていることを、お分かりいただけたでしょうか。

謎や神秘に満ちあふれる
数学の面白さ

――では、数学を学ぶことの「面白さ」を教えてください。

数学は生きる上で役立つだけでなく、ゲームを解くような楽しさもありますし、謎を解明する面白さもあります。

「フェルマーの最終定理」をご存じでしょうか？ 「3以上の自然数nについて、xⁿ + yⁿ = zⁿとなる自然数の組 (x, y, z) は存在しない」というものです。nに2を当てはめるとピタゴラスの定理になりますが、3以上になると、見つからないんですね。「存在しない」ことを示す定理なので、実生活ではほとんど役に立ちません。

しかし、この定理を証明しようと、17世紀以来、数多くの数学者が挑戦してきました。この研究が発端となって「代数幾何学」や「楕円(だえん)曲線」といった副次的な分野も発展しています。そして1994年、ワイルズという数学者によって、ようやく証明されたのです。

フェルマーの最終定理が、なぜ研究者ではない人も巻き込んだのか？　それは極めてシンプルであるにもかかわらず、証明が困難であるからでしょう。数学界にはこのような、ロマンあふれる謎が多数あります。

また、数学は神秘的なところにも魅力があります。私は仏像の構図を見るのが趣味なのですが、阿弥陀(あみだ)三尊像や薬師如来像は、左右の対称性が非常に高い。人間は対称性のあるものを美しいと感じます。むしろ高貴だと感じるあまり、近づきがたくなるほどで、例えば、正確に近い左右対称の顔の役者は大スターになることが少ないんです。私は芸能人の顔を見て、「この人は売れるな」と予想するのも趣味です（笑）。

しかしなぜ、仏像を作った彫刻家たちは、測るわけでもなく自然と左右対称を目指していたのでしょうか。もしかしたら私たち人間は、もともと本質的な部分に数学的能力を潜ませているのかもしれません。「古代人や動植物にも数学的な先天性が備わっているのだろうか？」「なぜ、ギザのピラミッドには『黄金分割』が用いられているのか？」「多くの植物において葉の付き方が『フィボナッチ数列』で決まっているのはなぜか？」...と、想像力をかきたてる神秘的な謎が多数あります。私はそうしたことに、ロマンのようなものを感じます。

数学が苦手な人は、
学び方や順番を間違えている!?

――柳谷先生は、昔から数学が得意だったのでしょうか？

実は私、数学の点数はさほど高くありませんでした。特に図形は苦手分野。数学少年というよりも、天文学や歴史などが好きだったんです。最初は天文学者になろうと思ったのですが、体が弱く、観測などの実地活動に向いていないことから、数学の道を歩み始めました。ただ、疲れているときに数式を眺めると落ち着くような、おかしな嗜好(しこう)は昔からありましたね（笑）。

幼い頃の幅広い興味は、現在、講義や執筆活動をする上で役に立っています。数学が何に役立つかを、社会問題や自然環境、歴史や文化に絡めて話すと、皆さんも理解しやすいんです。

特に、数学を面白く伝える書籍の執筆は、私のライフワークになっています。企業で働く方々は、ビジネスに触れる中で統計などに対するリテラシーを身に付けられるかもしれません。しかし、そうでない方々は、しっかりと数学を学ぶ時間を確保できるのでしょうか？ 誰もが社会にだまされないために、少しでも面白く学べる本を作って、数学の知識を還元する。私はそこにやりがいを感じますし、大切に続けていきたい仕事の１つです。

――なぜ数学を苦手とする学生が多いのでしょうか？

長年教員をやっている経験からすると、数学が苦手な学生は、「人の言うことを素直に聞かない、」「知らない癖に思い込みが強い」といったタイプが多いのかもしれません（笑）。これって、学生さんだけではありませんが。

数学の勉強は、先人たちの努力の礎の上に立つ、道具として仕上がった領域です。それを自己流で学ぶことはできないんです。例えば地理では、北海道から南へ学ぼうが、沖縄から北に学ぼうが、習熟度に差は出ないと思います。しかし、数学はそれが許されない。加法定理を知らない生徒に、三角関数の微分積分は計算できません。そこを間違えたら、ずっと数学が苦手のままになってしまいます。

しかし、学ぶことに“手遅れ”はありません。本に書いていること、教師の言っていることを素直に聞き、繰り返し練習すれば、数学は必ず誰でもできるようになります。まずは、「こんなものが何の役に立つのか？」「いち早く簡単に習得したい！」といった雑念を取り払いましょう。専門用語をしっかりと調べ、公式を正確に暗記しながら、一つ一つゆっくりと、積み上げるように学ぶことが、最終的には近道になります。

現在、数学から離れている場合、高校レベルの微分積分までをもう一度復習すれば、社会に出たときにかなり大きな力になると思います。その後の難しい数学は、若いうちに全てを詰め込もうとせず、小説をのんびり読むように、生涯をかけて学べば大丈夫です。一度はまると、楽しいものですよ。